The picture above is a 3d wireframe exploded view model of synaptic vesicles and synapses courtesy of National Geographic's youtube channel. The picture is from a segment on how our brains communicate at the tiniest scale.
The resources I will be using include Stephen Welch's great lecture on Neural Networks, the Interactive Python book, and Patrick Winston's lectures on Artificial Intelligence along with the accompanying textbook.
The Middle
I am fascinated by how things work. Computer Science gives one an outlet for this fascination, and the ability to model things and discover how they work. In the words of MIT Artificial Intelligence Professor Patrick Winston, making models allows one to "understand the past, predict the future, and control the world."
One thing I have been trying to figure out for quite some time is how my brain works...
I think the most interesting place to begin answering how our brains work, or more specifically how artificial neural networks work, is by comparing how we are different than the chimpanzees whom we share approximately 96 percent of our dna with. Most people would come to the conclusion that over the course of evolution, slow steady improvement eventually made our brains better than those of the chimpanzees. According to Professor Winston, this is not the case. "From the fossil record, the story seems to be this. We humans have been around for about 200,000 years in our present anatomical form. However, for the first 150,000 years or so humans did not amount to much. Somehow, shortly before 50,000 years ago, one small group of us developed a capability that seperated us from all other species. It was an accident of evolution. It is also probably the case that we necked down as a species to a few thousand or few hundred individuals, something that made these accidental evolutionary changes more capable of sticking... This leads us to speculate on what it was that happened 50,000 years ago. Paleoanthropologists, Noam Chomsky, and many others have reached a similar conclusion." To quote Chomsky, "It seems that shortly before 50,000 years ago, some small group of us developed the ability to take two concepts, and combine them to make a third concept, without disturbing the original two concepts; without limit."
Winston declares that what Chomsky is saying is we began to learn how to describe things in a way that was intimately connected with language, and that in the end is what seperates us from chimpanzees.

"So you might think lets just study language. You can't do that because we actually think with our eyes. According to Winston, language does two things. Number one it enables us to make descriptions, descriptions enable us to tell stories, and story telling and story understanding is what all of learning is about. Number two, language enables us to marshal the resources of our perceptual systems, and even command our perceptual systems to imagine things we have never seen!"
To reference one of our previous examples, Theodorus had at his disposal sticks and sand. He took one stick, and another stick of equal length, and put them together at a right angle. Through sticks and sand he was able to communicate and derive many mathematical concepts.
In computer science we extend this concept to model pretty much anything. The next section of this Ipython Notebook is going to be a study of how we model most things in Python up to human intelligence. This is the hard part. Humans are incredible at noticing patterns and pattern recognition, and it takes many neurons to perform these calculations. Lets start off by modeling a basic data structure that we now know the Egyptians came up with, Fractions.
Classes
As you may know, a fraction has a numerator and a denominator. We will initialize our class with these values.
%pylab inline
class Fraction:
def __init__(self,numerator,denominator):
self.num = numerator
self.den = denominator
Now we need a way to display our fraction in Ipython.
def show(self):
print(self.num,"/",self.den)
Putting it together,
class Fraction:
def __init__(self,numerator,denominator):
self.num = numerator
self.den = denominator
def show(self):
print(self.num,"/",self.den)
newFraction = Fraction(1,1)
newFraction.show()
print(newFraction)
Now we need a string function for our fraction.
def __str__(self):
return str(self.num)+"/"+str(self.den)
class Fraction:
def __init__(self,numerator,denominator):
self.num = numerator
self.den = denominator
def show(self):
print(self.num,"/",self.den)
def __str__(self):
return str(self.num)+"/"+str(self.den)
newFraction = Fraction(1,1)
newFraction.show()
print(newFraction)
In addition to the above functions, we also need a way to add two fraction objects together.
def __add__(self,otherfraction):
newnum = self.num*otherfraction.den + self.den*otherfraction.num
newden = self.den * otherfraction.den
return Fraction(newnum,newden)
class Fraction:
def __init__(self,numerator,denominator):
self.num = numerator
self.den = denominator
def show(self):
print(self.num,"/",self.den)
def __str__(self):
return str(self.num)+"/"+str(self.den)
def __add__(self,otherfraction):
newnum = self.num*otherfraction.den + self.den*otherfraction.num
newden = self.den * otherfraction.den
return Fraction(newnum,newden)
f1 = Fraction(1,2)
f2 = Fraction(1,2)
print(f1 + f2)
The addition function works, but it is not returning the fraction with the least common denominator, which in our case would be 1/1, or 1. This is where programming becomes powerful to users. We can modify our method to return what we want using logic. Additionally, notice that I am not calling an addition function, but rather the addition operator. What we are doing is referred to as overloading primitive operators. Python let's us change the behavior of it's built in classes in relation to our predefined fraction class. Next, let's define a function that returns the greatest common denominator of our fractions.
def gcd(m,n):
while m%n != 0:
oldm = m
oldn = n
m = oldn
n = oldm%oldn
return n
print(gcd(20,10))
Buenisimo! Now, let's modify our addition function.
def gcd(m,n):
while m%n != 0:
oldm = m
oldn = n
m = oldn
n = oldm%oldn
return n
class Fraction:
def __init__(self,numerator,denominator):
self.num = numerator
self.den = denominator
def show(self):
print(self.num,"/",self.den)
def __str__(self):
return str(self.num)+"/"+str(self.den)
def __add__(self,otherfraction):
newnum = self.num*otherfraction.den + self.den*otherfraction.num
newden = self.den * otherfraction.den
common = gcd(newnum,newden)
return Fraction(newnum//common,newden//common)
f1 = Fraction(10,20)
f2 = Fraction(10,20)
print(f1 + f2)
Now that we have addition fully operational, let's work on subtraction, multiplication, and division.
def gcd(m,n):
while m%n != 0:
oldm = m
oldn = n
m = oldn
n = oldm%oldn
return n
class Fraction:
def __init__(self,numerator,denominator):
self.num = numerator
self.den = denominator
def show(self):
print(self.num,"/",self.den)
def __str__(self):
return str(self.num)+"/"+str(self.den)
def __add__(self,otherfraction):
newnum = self.num*otherfraction.den + self.den*otherfraction.num
newden = self.den * otherfraction.den
common = gcd(newnum,newden)
return Fraction(newnum//common,newden//common)
def __sub__(self,otherfraction):
newnum = self.num*otherfraction.den - self.den*otherfraction.num
newden = self.den * otherfraction.den
common = gcd(newnum,newden)
return Fraction(newnum//common,newden//common)
def __mul__(self,otherfraction):
newnum = self.num*otherfraction.num
newden = self.den * otherfraction.den
common = gcd(newnum,newden)
return Fraction(newnum//common,newden//common)
#We need to specify if we want to overload the // operator, floor div or the / operator, true div.
def __truediv__(self,otherfraction):
newnum = self.num*otherfraction.den
newden = self.den * otherfraction.num
common = gcd(newnum,newden)
return Fraction(newnum//common,newden//common)
f1 = Fraction(20,10)
f2 = Fraction(10,10)
print(f1 - f2)
print(f1 * f2)
print(f1 / f2)
Our fraction class appears to be working correctly so far. Now, let's overload the comparison operators like equality, greater than, and less than.
def gcd(m,n):
while m%n != 0:
oldm = m
oldn = n
m = oldn
n = oldm%oldn
return n
class Fraction:
def __init__(self,numerator,denominator):
self.num = numerator
self.den = denominator
def show(self):
print(self.num,"/",self.den)
def __str__(self):
return str(self.num)+"/"+str(self.den)
def __add__(self,otherfraction):
newnum = self.num*otherfraction.den + self.den*otherfraction.num
newden = self.den * otherfraction.den
common = gcd(newnum,newden)
return Fraction(newnum//common,newden//common)
def __sub__(self,otherfraction):
newnum = self.num*otherfraction.den - self.den*otherfraction.num
newden = self.den * otherfraction.den
common = gcd(newnum,newden)
return Fraction(newnum//common,newden//common)
def __mul__(self,otherfraction):
newnum = self.num*otherfraction.num
newden = self.den * otherfraction.den
common = gcd(newnum,newden)
return Fraction(newnum//common,newden//common)
#We need to specify if we want to overload the // operator, floor div or the / operator, true div.
def __truediv__(self,otherfraction):
newnum = self.num*otherfraction.den
newden = self.den * otherfraction.num
common = gcd(newnum,newden)
return Fraction(newnum//common,newden//common)
def __eq__(self, other):
firstnum = self.num * other.den
secondnum = other.num * self.den
return firstnum == secondnum
def __ne__(self, other):
firstnum = self.num * other.den
secondnum = other.num * self.den
return firstnum != secondnum
def __lt__(self, other):
firstnum = self.num * other.den
secondnum = other.num * self.den
return firstnum < secondnum
def __gt__(self, other):
firstnum = self.num * other.den
secondnum = other.num * self.den
return firstnum > secondnum
f1 = Fraction(1,1)
f2 = Fraction(1,2)
print(f1 == f2)
print(f1 != f2)
print(f1 < f2)
print(f1 > f2)
Excellent! Of course, there are far more operators we could overload if we wanted to. For now, however, This class has presented the basic idea of how malleable programming can be. Now let's move on to stacks and linear data structures.
Stacks
A stack is a stack of stuff...literally. If you have a stack of books, thats a stack. Stacks obey LIFO logic, that is last in first out. This is because you can only put things on top of a stack and take things off of a stack. Putting things onto a stack is referred to as pushing, and taking an item off of the stack is referred to as popping. You can also 'peek' at the top item of the stack, and test if it 'isEmpty' and see it's 'size'. Let's program a stack using a python list.
class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def push(self, item):
self.items.insert(0,item)
def pop(self):
return self.items.pop(0)
def peek(self):
return self.items[0]
def size(self):
return len(self.items)
s = Stack()
print(s.isEmpty())
s.push(1)
print(s.isEmpty())
s.push(2)
s.push(3)
print(s.peek())
print(s.size())
s.pop()
print(s.peek())
print(s.size())
s.pop()
print(s.peek())
print(s.size())
s.pop()
print(s.isEmpty())
Queues
Queue's are similar to stacks, and opposite in logic. A queue is like a line at a grocery store, you add things to the end (enqueue) and pop things off the front (dequeue). This logic is referred to as FIFO. Let's implement a queue in python.
class Queue:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def enqueue(self, item):
self.items.insert(0,item)
def dequeue(self):
return self.items.pop()
def size(self):
return len(self.items)
#Some peeps in line
q = Queue()
print(q.size())
q.enqueue('Andrew')
q.enqueue('Bill')
q.enqueue('Colin')
print(q.size())
print(q.dequeue())
print(q.dequeue())
print(q.dequeue())
print(q.size())
Dequeue
A dequeue, apart from being an insane scrabble word to throw on top of queue, is a further extension of a queue. Dequeues allow you to add things and remove things from the front and rear. A dequeue is actually a more correct representation of people in line at a grocery store, as it allows for more than one line, and provides the ability to get off the end of a line and move to another. This is how scheduling works in your operating system. You have threads or processes that get in lines on your processors, and if the processor is busy with that line, and the size is large, you move to another line that is shorter or not busy. I may go into scheduling a little later on, but for now let's build a basic dequeue.
class Dequeue:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def addFront(self, item):
self.items.append(item)
def addRear(self, item):
self.items.insert(0,item)
def removeFront(self):
return self.items.pop()
def removeRear(self):
return self.items.pop(0)
def size(self):
return len(self.items)
d = Dequeue()
print(d.isEmpty())
d.addFront('Bill')
d.addFront('Andrew')
d.addRear('Colin')
print(d.size())
print(d.removeFront())
print(d.removeRear())
print(d.size())
print(d.removeRear())
print(d.size())
Unordered List
#TO DO!
class Node:
def __init__(self,initdata):
self.data = initdata
self.next = None
def getData(self):
return self.data
def getNext(self):
return self.next
def setData(self,newdata):
self.data = newdata
def setNext(self,newnext):
self.next = newnext
temp = Node(1)
temp.getData()
class UnorderedList:
def __init__(self):
self.head = None
def isEmpty(self):
return self.head == None
def add(self,item):
temp = Node(item)
temp.setNext(self.head)
self.head = temp
def size(self):
current = self.head
count = 0
while current != None:
count = count + 1
current = current.getNext()
return count
def search(self,item):
current = self.head
found = False
while current != None and not found:
if current.getData() == item:
found = True
else:
current = current.getNext()
return found
def remove(self,item):
current = self.head
previous = None
found = False
while not found:
if current.getData() == item:
found = True
else:
previous = current
current = current.getNext()
if previous == None:
self.head = current.getNext()
else:
previous.setNext(current.getNext())
mylist = UnorderedList()
mylist.add(1)
mylist.add(2)
mylist.add(3)
mylist.add(4)
mylist.add(5)
mylist.add(6)
print(mylist.isEmpty())
print(mylist.search(4))
print(mylist.size())
mylist.remove(4)
print(mylist.search(4))
print(mylist.size())
Ordered List
#TO DO!
class Node:
def __init__(self,initdata):
self.data = initdata
self.next = None
def getData(self):
return self.data
def getNext(self):
return self.next
def setData(self,newdata):
self.data = newdata
def setNext(self,newnext):
self.next = newnext
class OrderedList:
def __init__(self):
self.head = None
def isEmpty(self):
return self.head == None
def add(self,item):
current = self.head
previous = None
stop = False
while current != None and not stop:
if current.getData() > item:
stop = True
else:
previous = current
current = current.getNext()
temp = Node(item)
if previous == None:
temp.setNext(self.head)
self.head = temp
else:
temp.setNext(current)
previous.setNext(temp)
def size(self):
current = self.head
count = 0
while current != None:
count = count + 1
current = current.getNext()
return count
def search(self,item):
current = self.head
found = False
stop = False
while current != None and not found and not stop:
if current.getData() == item:
found = True
else:
if current.getData() > item:
stop = True
else:
current = current.getNext()
return found
def remove(self,item):
current = self.head
previous = None
found = False
while not found:
if current.getData() == item:
found = True
else:
previous = current
current = current.getNext()
if previous == None:
self.head = current.getNext()
else:
previous.setNext(current.getNext())
mylist = OrderedList()
mylist.add(1)
mylist.add(2)
mylist.add(3)
mylist.add(4)
mylist.add(5)
mylist.add(6)
print(mylist.isEmpty())
print(mylist.search(4))
print(mylist.size())
mylist.remove(4)
print(mylist.search(4))
print(mylist.size())
Recursion
#TO DO!
Searching and Sorting
#TO DO!
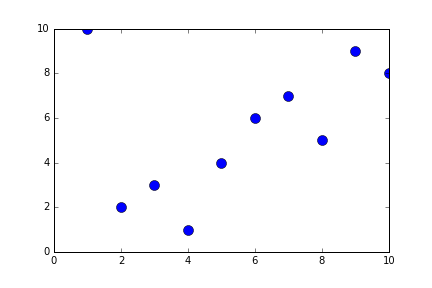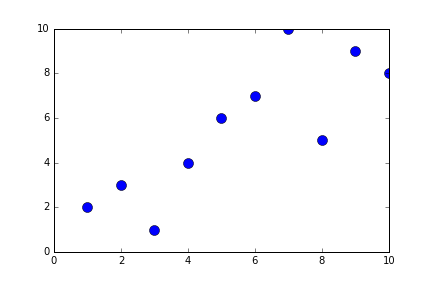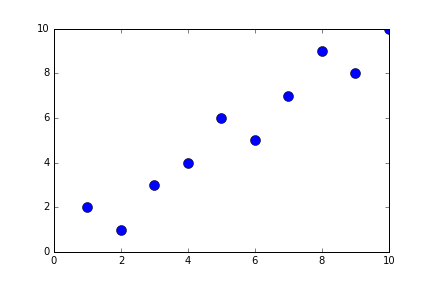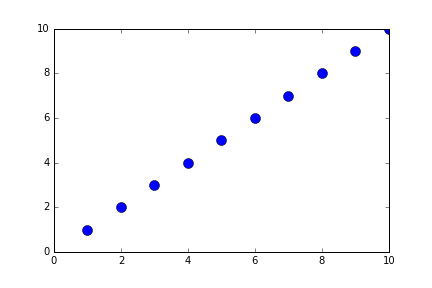
def generateBubbleSort(alist):
newListOfLists = []
for passnum in range(len(alist)-1,0,-1):
newListOfLists.append(list(alist))
for i in range(passnum):
if alist[i]>alist[i+1]:
temp = alist[i]
alist[i] = alist[i+1]
alist[i+1] = temp
newListOfLists.append(list(alist))
return newListOfLists
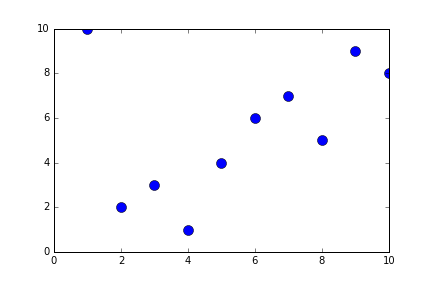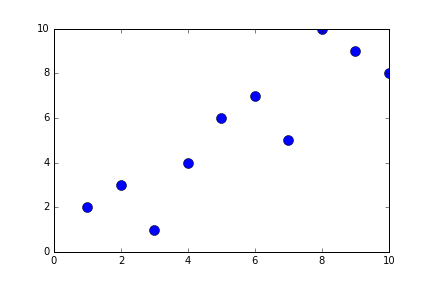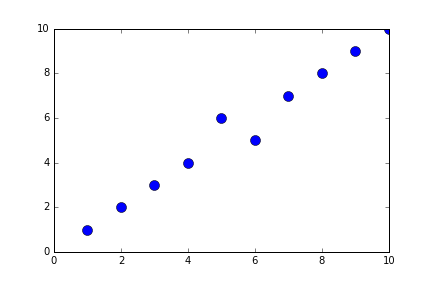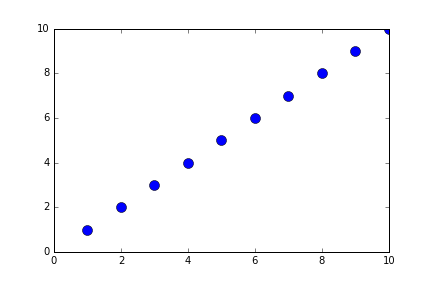
alist = [10,2,3,5,1,4,6,7,9,8]
newListOfLists = generateBubbleSort(alist)
print(newListOfLists)
print(len(newListOfLists))
from JSAnimation.IPython_display import display_animation
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
#fig, ax = plt.subplots()
#alist = [10, 2 ,3 ,1 , 4, 6, 7, 5, 9, 8]
#newListOfLists = generateBubbleSort(alist)
#print(newListOfLists)
#print(len(newListOfLists))
#line1, = ax.plot([], [], 'bo', ms=10)
#line2, = ax.plot([], [], 'bo', ms=10)
#line3, = ax.plot([], [], 'bo', ms=10)
#line4, = ax.plot([], [], 'bo', ms=10)
#line5, = ax.plot([], [], 'bo', ms=10)
#line6, = ax.plot([], [], 'bo', ms=10)
#line7, = ax.plot([], [], 'bo', ms=10)
#line8, = ax.plot([], [], 'bo', ms=10)
#line9, = ax.plot([], [], 'bo', ms=10)
#line10, = ax.plot([], [], 'bo', ms=10)
#Set y axes
#ax.set_ylim(0, 10)
#Set x axes
#ax.set_xlim(0, 10)
def animate(i):
line1.set_data(1,newListOfLists[i//10][0]) # update the data
line2.set_data(2,newListOfLists[i//10][1]) # update the data
line3.set_data(3,newListOfLists[i//10][2]) # update the data
line4.set_data(4,newListOfLists[i//10][3]) # update the data
line5.set_data(5,newListOfLists[i//10][4]) # update the data
line6.set_data(6,newListOfLists[i//10][5]) # update the data
line7.set_data(7,newListOfLists[i//10][6]) # update the data
line8.set_data(8,newListOfLists[i//10][7]) # update the data
line9.set_data(9,newListOfLists[i//10][8]) # update the data
line10.set_data(10,newListOfLists[i//10][9]) # update the data
return line1, line2, line3, line4, line5, line6, line7, line8, line9, line10
# Init only required for blitting to give a clean slate.
def init():
line1.set_data([],[]) # update the data
line2.set_data([],[]) # update the data
line3.set_data([],[]) # update the data
line4.set_data([],[]) # update the data
line5.set_data([],[]) # update the data
line6.set_data([],[]) # update the data
line7.set_data([],[]) # update the data
line8.set_data([],[]) # update the data
line9.set_data([],[]) # update the data
line10.set_data([],[]) # update the data
return line1, line2, line3, line4, line5, line6, line7, line8, line9, line10
#ani = animation.FuncAnimation(fig, animate, np.arange(1, 230), init_func=init, interval=25, blit=True)
#display_animation(ani, default_mode='once')
#ani.save('BubbleSort.gif', writer='imagemagick')
def generateShortBubbleSort(alist):
newListOfLists = []
exchanges = True
passnum = len(alist)-1
while passnum > 0 and exchanges:
newListOfLists.append(list(alist))
exchanges = False
for i in range(passnum):
if alist[i]>alist[i+1]:
exchanges = True
temp = alist[i]
alist[i] = alist[i+1]
alist[i+1] = temp
newListOfLists.append(list(alist))
passnum = passnum-1
return newListOfLists
alist = [10,2,3,1,4,6,7,9,8]
newListOfLists = generateShortBubbleSort(alist)
print(newListOfLists)
from JSAnimation.IPython_display import display_animation
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
#fig, ax = plt.subplots()
#alist = [10, 2 ,3 ,1 , 4, 6, 7, 5, 9, 8]
#newListOfLists = generateShortBubbleSort(alist)
#print(newListOfLists)
#print(len(newListOfLists))
#line1, = ax.plot([], [], 'bo', ms=10)
#line2, = ax.plot([], [], 'bo', ms=10)
#line3, = ax.plot([], [], 'bo', ms=10)
#line4, = ax.plot([], [], 'bo', ms=10)
#line5, = ax.plot([], [], 'bo', ms=10)
#line6, = ax.plot([], [], 'bo', ms=10)
#line7, = ax.plot([], [], 'bo', ms=10)
#line8, = ax.plot([], [], 'bo', ms=10)
#line9, = ax.plot([], [], 'bo', ms=10)
#line10, = ax.plot([], [], 'bo', ms=10)
#Set y axes
#ax.set_ylim(0, 10)
#Set x axes
#ax.set_xlim(0, 10)
def animate(i):
line1.set_data(1,newListOfLists[i//10][0]) # update the data
line2.set_data(2,newListOfLists[i//10][1]) # update the data
line3.set_data(3,newListOfLists[i//10][2]) # update the data
line4.set_data(4,newListOfLists[i//10][3]) # update the data
line5.set_data(5,newListOfLists[i//10][4]) # update the data
line6.set_data(6,newListOfLists[i//10][5]) # update the data
line7.set_data(7,newListOfLists[i//10][6]) # update the data
line8.set_data(8,newListOfLists[i//10][7]) # update the data
line9.set_data(9,newListOfLists[i//10][8]) # update the data
line10.set_data(10,newListOfLists[i//10][9]) # update the data
return line1, line2, line3, line4, line5, line6, line7, line8, line9, line10
# Init only required for blitting to give a clean slate.
def init():
line1.set_data([],[]) # update the data
line2.set_data([],[]) # update the data
line3.set_data([],[]) # update the data
line4.set_data([],[]) # update the data
line5.set_data([],[]) # update the data
line6.set_data([],[]) # update the data
line7.set_data([],[]) # update the data
line8.set_data([],[]) # update the data
line9.set_data([],[]) # update the data
line10.set_data([],[]) # update the data
return line1, line2, line3, line4, line5, line6, line7, line8, line9, line10
#ani = animation.FuncAnimation(fig, animate, np.arange(1, 180), init_func=init,
# interval=25, blit=True)
#display_animation(ani, default_mode='once')
#ani.save('ShortBubbleSort.gif', writer='imagemagick')
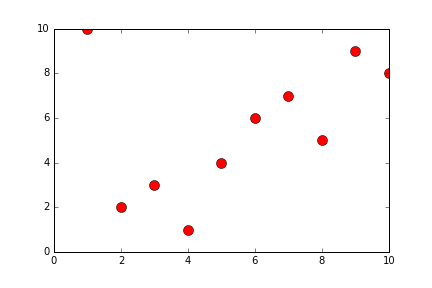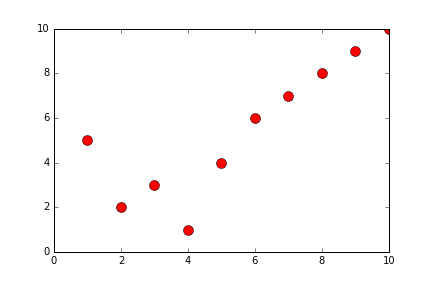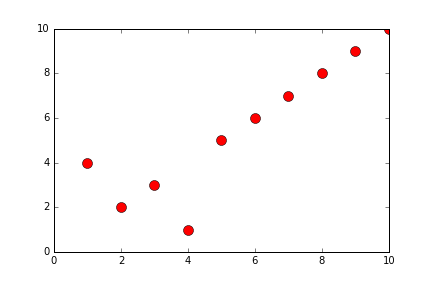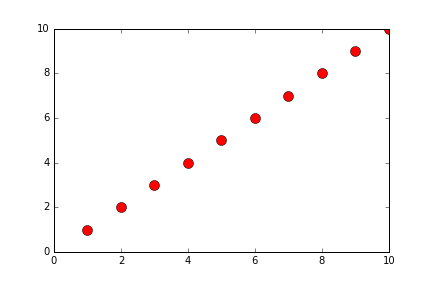
def generateSelectionSort(alist):
newListOfLists = []
for fillslot in range(len(alist)-1,0,-1):
newListOfLists.append(list(alist))
positionOfMax=0
for location in range(1,fillslot+1):
if alist[location]>alist[positionOfMax]:
positionOfMax = location
newListOfLists.append(list(alist))
temp = alist[fillslot]
alist[fillslot] = alist[positionOfMax]
alist[positionOfMax] = temp
return newListOfLists
alist = [10,2,3,1,4,6,7,9,8]
newListOfLists = generateSelectionSort(alist)
print(newListOfLists)
from JSAnimation.IPython_display import display_animation
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
#fig, ax = plt.subplots()
#alist = [10, 2 ,3 ,1 , 4, 6, 7, 5, 9, 8]
#newListOfLists = generateSelectionSort(alist)
#print(newListOfLists)
#print(len(newListOfLists))
#line1, = ax.plot([], [], 'ro', ms=10)
#line2, = ax.plot([], [], 'ro', ms=10)
#line3, = ax.plot([], [], 'ro', ms=10)
#line4, = ax.plot([], [], 'ro', ms=10)
#line5, = ax.plot([], [], 'ro', ms=10)
#line6, = ax.plot([], [], 'ro', ms=10)
#line7, = ax.plot([], [], 'ro', ms=10)
#line8, = ax.plot([], [], 'ro', ms=10)
#line9, = ax.plot([], [], 'ro', ms=10)
#line10, = ax.plot([], [], 'ro', ms=10)
#Set y axes
#ax.set_ylim(0, 10)
#Set x axes
#ax.set_xlim(0, 10)
def animate(i):
line1.set_data(1,newListOfLists[i//10][0]) # update the data
line2.set_data(2,newListOfLists[i//10][1]) # update the data
line3.set_data(3,newListOfLists[i//10][2]) # update the data
line4.set_data(4,newListOfLists[i//10][3]) # update the data
line5.set_data(5,newListOfLists[i//10][4]) # update the data
line6.set_data(6,newListOfLists[i//10][5]) # update the data
line7.set_data(7,newListOfLists[i//10][6]) # update the data
line8.set_data(8,newListOfLists[i//10][7]) # update the data
line9.set_data(9,newListOfLists[i//10][8]) # update the data
line10.set_data(10,newListOfLists[i//10][9]) # update the data
return line1, line2, line3, line4, line5, line6, line7, line8, line9, line10
# Init only required for blitting to give a clean slate.
def init():
line1.set_data([],[]) # update the data
line2.set_data([],[]) # update the data
line3.set_data([],[]) # update the data
line4.set_data([],[]) # update the data
line5.set_data([],[]) # update the data
line6.set_data([],[]) # update the data
line7.set_data([],[]) # update the data
line8.set_data([],[]) # update the data
line9.set_data([],[]) # update the data
line10.set_data([],[]) # update the data
return line1, line2, line3, line4, line5, line6, line7, line8, line9, line10
#ani = animation.FuncAnimation(fig, animate, np.arange(1, 160), init_func=init,
# interval=25, blit=True)
#display_animation(ani, default_mode='once')
#ani.save('SelectionSort.gif', writer='imagemagick')
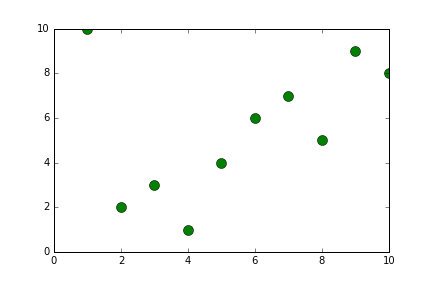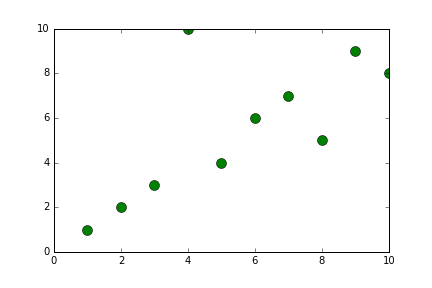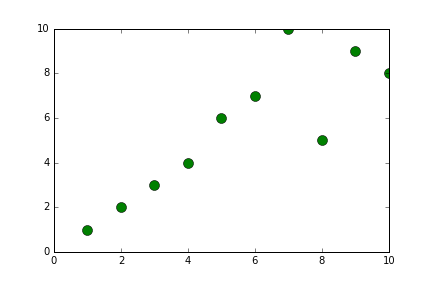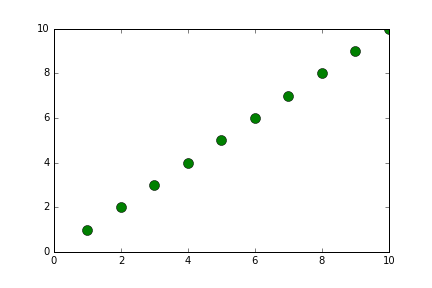
def generateInsertionSort(alist):
newListOfLists = []
for index in range(1,len(alist)):
newListOfLists.append(list(alist))
currentvalue = alist[index]
position = index
while position>0 and alist[position-1]>currentvalue:
alist[position]=alist[position-1]
position = position-1
alist[position]=currentvalue
newListOfLists.append(list(alist))
return newListOfLists
alist = [10,2,3,1,4,6,7,9,8]
newListOfLists = generateInsertionSort(alist)
print(newListOfLists)
print(len(newListOfLists))
from JSAnimation.IPython_display import display_animation
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
#fig, ax = plt.subplots()
#alist = [10, 2 ,3 ,1 , 4, 6, 7, 5, 9, 8]
#newListOfLists = generateInsertionSort(alist)
#print(newListOfLists)
#print(len(newListOfLists))
#line1, = ax.plot([], [], 'go', ms=10)
#line2, = ax.plot([], [], 'go', ms=10)
#line3, = ax.plot([], [], 'go', ms=10)
#line4, = ax.plot([], [], 'go', ms=10)
#line5, = ax.plot([], [], 'go', ms=10)
#line6, = ax.plot([], [], 'go', ms=10)
#line7, = ax.plot([], [], 'go', ms=10)
#line8, = ax.plot([], [], 'go', ms=10)
#line9, = ax.plot([], [], 'go', ms=10)
#line10, = ax.plot([], [], 'go', ms=10)
#Set y axes
#ax.set_ylim(0, 10)
#Set x axes
#ax.set_xlim(0, 10)
def animate(i):
line1.set_data(1,newListOfLists[i//10][0]) # update the data
line2.set_data(2,newListOfLists[i//10][1]) # update the data
line3.set_data(3,newListOfLists[i//10][2]) # update the data
line4.set_data(4,newListOfLists[i//10][3]) # update the data
line5.set_data(5,newListOfLists[i//10][4]) # update the data
line6.set_data(6,newListOfLists[i//10][5]) # update the data
line7.set_data(7,newListOfLists[i//10][6]) # update the data
line8.set_data(8,newListOfLists[i//10][7]) # update the data
line9.set_data(9,newListOfLists[i//10][8]) # update the data
line10.set_data(10,newListOfLists[i//10][9]) # update the data
return line1, line2, line3, line4, line5, line6, line7, line8, line9, line10
# Init only required for blitting to give a clean slate.
def init():
line1.set_data([],[]) # update the data
line2.set_data([],[]) # update the data
line3.set_data([],[]) # update the data
line4.set_data([],[]) # update the data
line5.set_data([],[]) # update the data
line6.set_data([],[]) # update the data
line7.set_data([],[]) # update the data
line8.set_data([],[]) # update the data
line9.set_data([],[]) # update the data
line10.set_data([],[]) # update the data
return line1, line2, line3, line4, line5, line6, line7, line8, line9, line10
#ani = animation.FuncAnimation(fig, animate, np.arange(1, 180), init_func=init,
# interval=25, blit=True)
#display_animation(ani, default_mode='once')
#ani.save('InsertionSort.gif', writer='imagemagick')
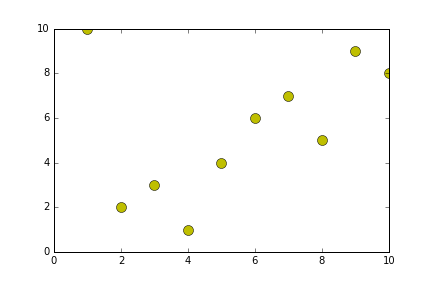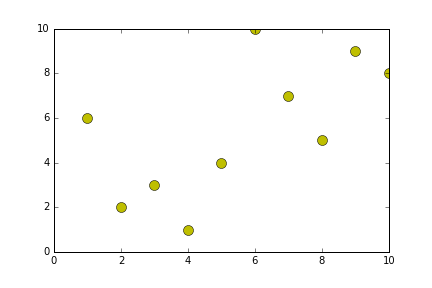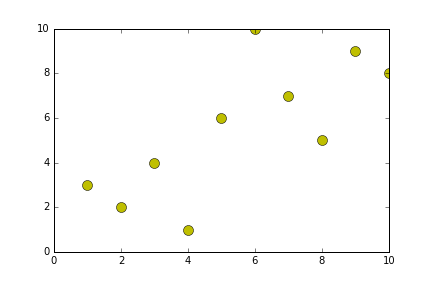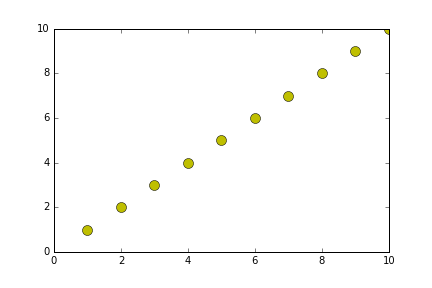
def generateShellSort(alist):
newListOfLists = []
sublistcount = len(alist)//2
while sublistcount > 0:
newListOfLists.append(list(alist))
for startposition in range(sublistcount):
gapInsertionSort(alist,startposition,sublistcount)
newListOfLists.append(list(alist))
sublistcount = sublistcount // 2
return newListOfLists
def gapInsertionSort(alist,start,gap):
for i in range(start+gap,len(alist),gap):
currentvalue = alist[i]
position = i
while position>=gap and alist[position-gap]>currentvalue:
alist[position]=alist[position-gap]
position = position-gap
alist[position]=currentvalue
alist = [10,2,3,1,4,6,7,9,8]
newListOfLists = generateShellSort(alist)
print(newListOfLists)
print(len(newListOfLists))
from JSAnimation.IPython_display import display_animation
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
#fig, ax = plt.subplots()
#alist = [10, 2 ,3 ,1 , 4, 6, 7, 5, 9, 8]
#newListOfLists = generateShellSort(alist)
#print(newListOfLists)
#print(len(newListOfLists))
#line1, = ax.plot([], [], 'yo', ms=10)
#line2, = ax.plot([], [], 'yo', ms=10)
#line3, = ax.plot([], [], 'yo', ms=10)
#line4, = ax.plot([], [], 'yo', ms=10)
#line5, = ax.plot([], [], 'yo', ms=10)
#line6, = ax.plot([], [], 'yo', ms=10)
#line7, = ax.plot([], [], 'yo', ms=10)
#line8, = ax.plot([], [], 'yo', ms=10)
#line9, = ax.plot([], [], 'yo', ms=10)
#line10, = ax.plot([], [], 'yo', ms=10)
#Set y axes
#ax.set_ylim(0, 10)
#Set x axes
#ax.set_xlim(0, 10)
def animate(i):
line1.set_data(1,newListOfLists[i//10][0]) # update the data
line2.set_data(2,newListOfLists[i//10][1]) # update the data
line3.set_data(3,newListOfLists[i//10][2]) # update the data
line4.set_data(4,newListOfLists[i//10][3]) # update the data
line5.set_data(5,newListOfLists[i//10][4]) # update the data
line6.set_data(6,newListOfLists[i//10][5]) # update the data
line7.set_data(7,newListOfLists[i//10][6]) # update the data
line8.set_data(8,newListOfLists[i//10][7]) # update the data
line9.set_data(9,newListOfLists[i//10][8]) # update the data
line10.set_data(10,newListOfLists[i//10][9]) # update the data
return line1, line2, line3, line4, line5, line6, line7, line8, line9, line10
# Init only required for blitting to give a clean slate.
def init():
line1.set_data([],[]) # update the data
line2.set_data([],[]) # update the data
line3.set_data([],[]) # update the data
line4.set_data([],[]) # update the data
line5.set_data([],[]) # update the data
line6.set_data([],[]) # update the data
line7.set_data([],[]) # update the data
line8.set_data([],[]) # update the data
line9.set_data([],[]) # update the data
line10.set_data([],[]) # update the data
return line1, line2, line3, line4, line5, line6, line7, line8, line9, line10
#ani = animation.FuncAnimation(fig, animate, np.arange(1, 110), init_func=init,
# interval=25, blit=True)
#display_animation(ani, default_mode='once')
#ani.save('ShellSort.gif', writer='imagemagick')
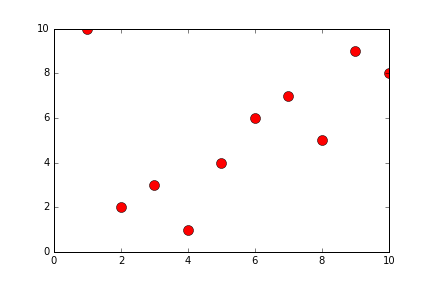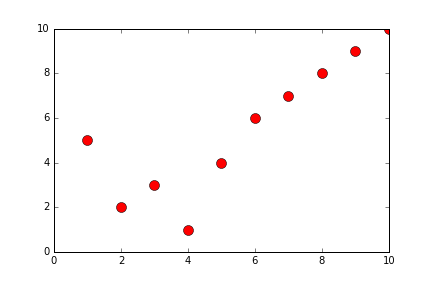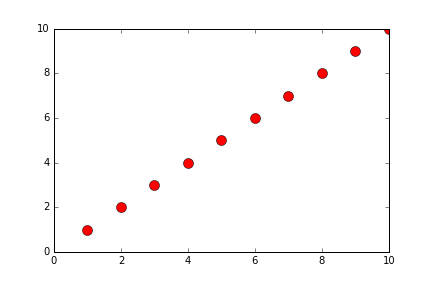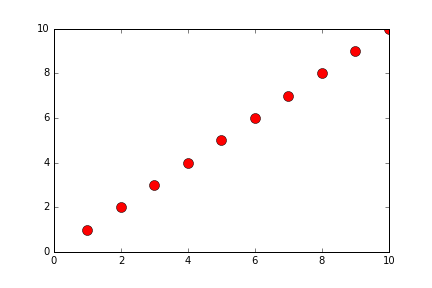
def generateQuickSort(alist):
quickSortHelper(alist,0,len(alist)-1)
return newListOfLists
def quickSortHelper(alist,first,last):
if first<last:
splitpoint = partition(alist,first,last)
quickSortHelper(alist,first,splitpoint-1)
quickSortHelper(alist,splitpoint+1,last)
def partition(alist,first,last):
pivotvalue = alist[first]
leftmark = first+1
rightmark = last
done = False
while not done:
while leftmark <= rightmark and alist[leftmark] <= pivotvalue:
leftmark = leftmark + 1
while alist[rightmark] >= pivotvalue and rightmark >= leftmark:
rightmark = rightmark -1
if rightmark < leftmark:
done = True
else:
temp = alist[leftmark]
alist[leftmark] = alist[rightmark]
alist[rightmark] = temp
temp = alist[first]
alist[first] = alist[rightmark]
alist[rightmark] = temp
newListOfLists.append(list(alist))
return rightmark
alist = [10,2,3,1,4,6,7,9,8]
newListOfLists = []
newListOfLists = generateQuickSort(alist)
print(newListOfLists)
print(len(newListOfLists))
from JSAnimation.IPython_display import display_animation
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
#fig, ax = plt.subplots()
#alist = [10, 2 ,3 ,1 , 4, 6, 7, 5, 9, 8]
#newListOfLists = []
#newListOfLists.append(list(alist))
#newListOfLists = generateQuickSort(alist)
#print(newListOfLists)
#print(len(newListOfLists))
#line1, = ax.plot([], [], 'ro', ms=10)
#line2, = ax.plot([], [], 'ro', ms=10)
#line3, = ax.plot([], [], 'ro', ms=10)
#line4, = ax.plot([], [], 'ro', ms=10)
#line5, = ax.plot([], [], 'ro', ms=10)
#line6, = ax.plot([], [], 'ro', ms=10)
#line7, = ax.plot([], [], 'ro', ms=10)
#line8, = ax.plot([], [], 'ro', ms=10)
#line9, = ax.plot([], [], 'ro', ms=10)
#line10, = ax.plot([], [], 'ro', ms=10)
#Set y axes
#ax.set_ylim(0, 10)
#Set x axes
#ax.set_xlim(0, 10)
def animate(i):
line1.set_data(1,newListOfLists[i//10][0]) # update the data
line2.set_data(2,newListOfLists[i//10][1]) # update the data
line3.set_data(3,newListOfLists[i//10][2]) # update the data
line4.set_data(4,newListOfLists[i//10][3]) # update the data
line5.set_data(5,newListOfLists[i//10][4]) # update the data
line6.set_data(6,newListOfLists[i//10][5]) # update the data
line7.set_data(7,newListOfLists[i//10][6]) # update the data
line8.set_data(8,newListOfLists[i//10][7]) # update the data
line9.set_data(9,newListOfLists[i//10][8]) # update the data
line10.set_data(10,newListOfLists[i//10][9]) # update the data
return line1, line2, line3, line4, line5, line6, line7, line8, line9, line10
# Init only required for blitting to give a clean slate.
def init():
line1.set_data([],[]) # update the data
line2.set_data([],[]) # update the data
line3.set_data([],[]) # update the data
line4.set_data([],[]) # update the data
line5.set_data([],[]) # update the data
line6.set_data([],[]) # update the data
line7.set_data([],[]) # update the data
line8.set_data([],[]) # update the data
line9.set_data([],[]) # update the data
line10.set_data([],[]) # update the data
return line1, line2, line3, line4, line5, line6, line7, line8, line9, line10
#ani = animation.FuncAnimation(fig, animate, np.arange(1, 80), init_func=init,
# interval=25, blit=True)
#display_animation(ani, default_mode='once')
#ani.save('QuickSort.gif', writer='imagemagick')
def BinaryTree(r):
return [r, [], []]
def insertLeft(root,newBranch):
t = root.pop(1)
if len(t) > 1:
root.insert(1,[newBranch,t,[]])
else:
root.insert(1,[newBranch, [], []])
return root
def insertRight(root,newBranch):
t = root.pop(2)
if len(t) > 1:
root.insert(2,[newBranch,[],t])
else:
root.insert(2,[newBranch,[],[]])
return root
def getRootVal(root):
return root[0]
def setRootVal(root,newVal):
root[0] = newVal
def getLeftChild(root):
return root[1]
def getRightChild(root):
return root[2]
r = BinaryTree(3)
insertLeft(r,4)
insertLeft(r,5)
insertRight(r,6)
insertRight(r,7)
l = getLeftChild(r)
print(l)
setRootVal(l,9)
print(r)
insertLeft(l,11)
print(r)
print(getRightChild(getRightChild(r)))
Coming Up
Good Will Hunting Problem
 </src>
</src>
Draw all homeomorphically irreducible trees of size n = 10.
%pylab inline
from matplotlib.path import Path
import matplotlib.patches as patches
verts = [
(-1.5, .5),
(-1.5, 0),
(-1.5, -.5),
(-1.5, 0),
(0, 0),
(-.5, .5),
(0, 0),
(-.5, -.5),
(0, 0),
(0, .5),
(0, 0),
(0, -.5),
(0, 0),
(.5, .5),
(0, 0),
(.5, -.5)
]
codes = [Path.MOVETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
]
path = Path(verts, codes)
fig = plt.figure()
ax = fig.add_subplot(111)
patch = patches.PathPatch(path, facecolor = 'White', lw=2)
ax.add_patch(patch)
ax.set_xlim(-2,2)
ax.set_ylim(-2,2)
plt.show()
%pylab inline
from matplotlib.path import Path
import matplotlib.patches as patches
verts = [
(-1.5, 0),
(-1, 0),
(-1, .5),
(-1, 0),
(-1, -.5),
(-1, 0),
(0, 0),
(-.5, -.5),
(0, 0),
(-.5, .5),
(0, 0),
(.5, 0),
(0, 0),
(.5, .5),
(0, 0),
(.5, -.5)
]
codes = [Path.MOVETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
]
path = Path(verts, codes)
fig = plt.figure()
ax = fig.add_subplot(111)
patch = patches.PathPatch(path, facecolor = 'White', lw=2)
ax.add_patch(patch)
ax.set_xlim(-2,2)
ax.set_ylim(-2,2)
plt.show()
%pylab inline
from matplotlib.path import Path
import matplotlib.patches as patches
verts = [
(-1, .5),
(-1, 0),
(-1, -.5),
(-1, 0),
(-.5, 0),
(-.5, .5),
(-.5, 0),
(-.5, -.5),
(-.5, 0),
(0, 0),
(0, .5),
(0, -.5),
(0, 0),
(.5, 0),
]
codes = [Path.MOVETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
]
path = Path(verts, codes)
fig = plt.figure()
ax = fig.add_subplot(111)
patch = patches.PathPatch(path, facecolor = 'White', lw=2)
ax.add_patch(patch)
ax.set_xlim(-2,2)
ax.set_ylim(-2,2)
plt.show()
%pylab inline
from matplotlib.path import Path
import matplotlib.patches as patches
verts = [
(-1.5, .5),
(-1.5, 0),
(-1.5, -.5),
(-1.5, 0),
(-.5, 0),
(-1, .5),
(-.5, 0),
(0, .5),
(-.5, 0),
(.5, 0),
(.5, .5),
(.5, -.5),
(.5, 0),
]
codes = [Path.MOVETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
]
path = Path(verts, codes)
fig = plt.figure()
ax = fig.add_subplot(111)
patch = patches.PathPatch(path, facecolor = 'White', lw=2)
ax.add_patch(patch)
ax.set_xlim(-2,2)
ax.set_ylim(-2,2)
plt.show()
%pylab inline
from matplotlib.path import Path
import matplotlib.patches as patches
verts = [
(-1.5, .5),
(-1.5, 0),
(-1.5, -.5),
(-1.5, 0),
(-1, 0),
(-1, 1.5),
(-1, 1),
(-.5, 1),
(-1, 1),
(-1, -.5),
(-1, -.5),
(-1, -.5),
(-.5, -.5),
(-1, -.5),
(-1, -1),
]
codes = [Path.MOVETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
]
path = Path(verts, codes)
fig = plt.figure()
ax = fig.add_subplot(111)
patch = patches.PathPatch(path, facecolor = 'White', lw=2)
ax.add_patch(patch)
ax.set_xlim(-2,2)
ax.set_ylim(-2,2)
plt.show()
%pylab inline
from matplotlib.path import Path
import matplotlib.patches as patches
verts = [
(-1.5, .5),
(-1, 0),
(-1.5, -.5),
(-1, 0),
(-1, .5),
(-1, 0),
(-1, -.5),
(-1, 0),
(0, 0),
(0, .5),
(0, 0),
(0, -.5),
(0, 0),
(.5, .5),
(0, 0),
(.5, -.5)
]
codes = [Path.MOVETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
]
path = Path(verts, codes)
fig = plt.figure()
ax = fig.add_subplot(111)
patch = patches.PathPatch(path, facecolor = 'White', lw=2)
ax.add_patch(patch)
ax.set_xlim(-2,2)
ax.set_ylim(-2,2)
plt.show()
%pylab inline
from matplotlib.path import Path
import matplotlib.patches as patches
verts = [
(-1.5, .5),
(-1.5, 0),
(-1.5, -.5),
(-1.5, 0),
(-1, 0),
(-1, -.5),
(-1, 0),
(-.5, 0),
(-.5, -.5),
(-.5, 0),
(0, 0),
(0, -.5),
(0, 0),
(0, .5),
(0, 0),
]
codes = [Path.MOVETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
]
path = Path(verts, codes)
fig = plt.figure()
ax = fig.add_subplot(111)
patch = patches.PathPatch(path, facecolor = 'White', lw=2)
ax.add_patch(patch)
ax.set_xlim(-2,2)
ax.set_ylim(-2,2)
plt.show()
%pylab inline
from matplotlib.path import Path
import matplotlib.patches as patches
verts = [
(-1, -1),
(0, 0),
(-1, -.5),
(0, 0),
(-1, 0),
(0, 0),
(-1, .5),
(0, 0),
(-1, 1),
(0, 0),
(0, 1),
(0, 0),
(0, 0),
(0, -1),
(0, 0),
(.5, 1),
(0, 0),
(.5, -1)
]
codes = [Path.MOVETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
]
path = Path(verts, codes)
fig = plt.figure()
ax = fig.add_subplot(111)
patch = patches.PathPatch(path, facecolor = 'White', lw=2)
ax.add_patch(patch)
ax.set_xlim(-2,2)
ax.set_ylim(-2,2)
plt.show()
%pylab inline
from matplotlib.path import Path
import matplotlib.patches as patches
verts = [
(-1.5, .5),
(-1.5, -.5),
(-1.5, 0),
(-.5, 0),
(-.5, .5),
(-.5, 0),
(0, 0),
(0, -.5),
(0, 0),
(0, .5),
(0, 0),
(.5, .5),
(0, 0),
(.5, -.5)
]
codes = [Path.MOVETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
]
path = Path(verts, codes)
fig = plt.figure()
ax = fig.add_subplot(111)
patch = patches.PathPatch(path, facecolor = 'White', lw=2)
ax.add_patch(patch)
ax.set_xlim(-2,2)
ax.set_ylim(-2,2)
plt.show()
%pylab inline
from matplotlib.path import Path
import matplotlib.patches as patches
verts = [
(-1.5, 0),
(-1, 0),
(-1, .5),
(-1, -.5),
(-1, 0),
(-.5, 0),
(-.5, .5),
(-.5, 0),
(0, 0),
(0, .5),
(0, 0),
(0, -.5),
(0, 0),
(.5, 0)
]
codes = [Path.MOVETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
Path.LINETO,
]
path = Path(verts, codes)
fig = plt.figure()
ax = fig.add_subplot(111)
patch = patches.PathPatch(path, facecolor = 'White', lw=2)
ax.add_patch(patch)
ax.set_xlim(-2,2)
ax.set_ylim(-2,2)
plt.show()
Databases
When one usually thinks of databases, they think of websites storing boring old data. This is sooooooooo wrong. Databases themselves are actually an incredibly complex and useful object. One of the coolest places databases are utilized is within language recognition. Natural language is very complex. Generally, when you have a command you want your computer to understand you have to translate it somehow so the computer understands you. Databases, specifically Relational Databases provide a gigantic piece of this puzzle as you will see in my example below.
Database designers and UI designers have come up for an acronym to describe the basic functions a database should provide. CRUD.
import sqlite3
#Initialize
connection = sqlite3.connect("newDB.db")
cursor = connection.cursor()
cursor.execute("""DROP TABLE Contacts;""")
sql_command = """CREATE TABLE Contacts (
Contact_ID INTEGER PRIMARY KEY,
First_Name VARCHAR(30),
Middle_Initial CHAR(1),
Last_Name VARCHAR(30),
Phone_Number VARCHAR(20));"""
#Create
cursor.execute(sql_command)
sql_command = """INSERT INTO Contacts (Contact_ID, First_Name, Middle_Initial, Last_Name, Phone_Number) VALUES (NULL, "John", "A", "Doe", "867-5309");"""
cursor.execute(sql_command)
sql_command = """INSERT INTO Contacts (Contact_ID, First_Name, Middle_Initial, Last_Name, Phone_Number) VALUES (NULL, "Ziggy", "A", "Stardust", "867-5309");"""
cursor.execute(sql_command)
# never forget this, if you want the changes to be saved:
connection.commit()
connection.close()
#Read
connection = sqlite3.connect("newDB.db")
cursor = connection.cursor()
cursor.execute("SELECT * FROM Contacts")
print("Read:")
result = cursor.fetchall()
for r in result:
print(r)
connection.close()
#Update
def Update(parameter, data, identifier1, identifier2):
#Initialize
connection = sqlite3.connect("newDB.db")
cursor = connection.cursor()
#Case (python3 does not provide switch statements, so we will use ifs)
if(parameter == "First_Name"):
command1 = 'SELECT FIRST_NAME FROM Contacts WHERE First_Name = "'\
+identifier1+'" AND Last_Name = "'+identifier2+'"'
print(command1)
cursor.execute(command1)
rows = cursor.fetchall()
for row in rows:
print ("%s" % (row[0]))
command2 = 'UPDATE Contacts SET First_Name = "'+data+'" WHERE First_Name = "'\
+identifier1+'" AND Last_Name = "'+identifier2+'"'
print(command2)
cursor.execute(command2)
command1 = 'SELECT FIRST_NAME FROM Contacts WHERE First_Name = "'\
+data+'" AND Last_Name = "'+identifier2+'"'
cursor.execute(command1)
rows = cursor.fetchall()
for row in rows:
print ("%s\n" % (row[0]))
elif(parameter == "Last_Name"):
command1 = 'SELECT Last_NAME FROM Contacts WHERE Last_Name = "'\
+identifier2+'" AND First_Name = "'+identifier1+'"'
print(command1)
cursor.execute(command1)
rows = cursor.fetchall()
for row in rows:
print ("%s" % (row[0]))
command2 = 'UPDATE Contacts SET Last_Name = "'+data+'" WHERE First_Name = "'\
+identifier1+'" AND Last_Name = "'+identifier2+'"'
print(command2)
cursor.execute(command2)
command1 = 'SELECT Last_NAME FROM Contacts WHERE Last_Name = "'\
+data+'" AND First_Name = "'+identifier1+'"'
cursor.execute(command1)
rows = cursor.fetchall()
for row in rows:
print ("%s\n" % (row[0]))
elif(parameter == "Phone_Number"):
command1 = 'SELECT Phone_Number FROM Contacts WHERE First_Name = "'\
+identifier1+'" AND Last_Name = "'+identifier2+'"'
print(command1)
cursor.execute(command1)
rows = cursor.fetchall()
for row in rows:
print ("%s" % (row[0]))
command2 = 'UPDATE Contacts SET Phone_Number = "'+data+'" WHERE First_Name = "'\
+identifier1+'" AND Last_Name = "'+identifier2+'"'
print(command2)
cursor.execute(command2)
command1 = 'SELECT Phone_Number FROM Contacts WHERE Phone_Number = "'\
+data+'"'
cursor.execute(command1)
rows = cursor.fetchall()
for row in rows:
print ("%s\n" % (row[0]))
connection.close()
Update("First_Name", "Moon Unit", "John", "Doe")
Update("Last_Name", "Zappa", "John", "Doe")
Update("Phone_Number", "1-800-MYLEMON", "John", "Doe")
#Delete
def Delete(identifier1, identifier2):
#Initialize
connection = sqlite3.connect("newDB.db")
cursor = connection.cursor()
command1 = 'DELETE FROM Contacts WHERE First_Name = "'\
+identifier1+'" AND Last_Name = "'+identifier2+'"'
print(command1)
cursor.execute(command1)
command1 = 'SELECT * FROM Contacts'
cursor.execute(command1)
result = cursor.fetchall()
print("Read:\n")
for r in result:
print(r)
connection.close()
Delete("John", "Doe")
Artificial Intelligence
Data and Architecture
Before we begin building our neural network, we need to look at some naive biology to base the mechanics of our model on.
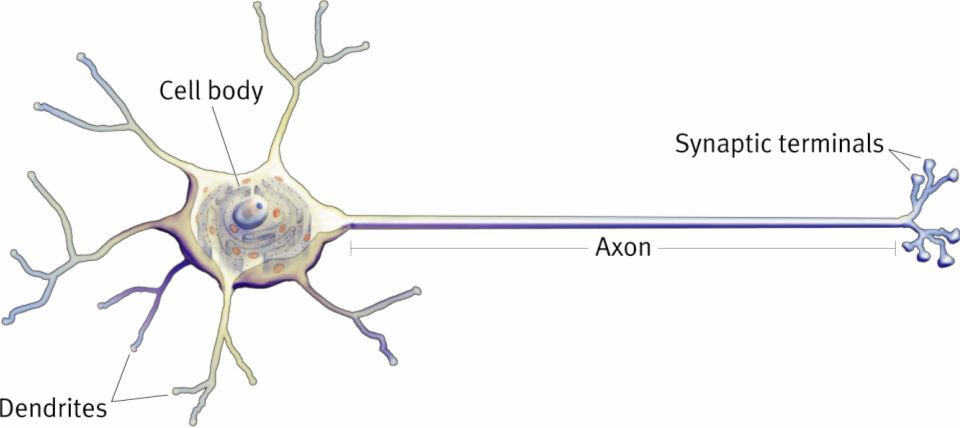
Neurons and neuroscience are obviously incredibly complex subjects, so for our network we are going to abstract the basic concept of two specific and similar neurons, the artificial neuron and the perceptron (or sigmoid neuron). To quote Winston's textbook, Artificial Intelligence, "most neurons, like the one shown [above] consist of a cell body plus one axon and many dendrites. The axon is a protuberance that delivers the neuron's output to connections with other neurons. Dendrites are protuberances that provide plenty of surface area, facilitating connection with the axons of other neurons. Dendrites often divide a great deal, forming extremely bushy dendritic trees. Axons divide to some extent, but far less than dendrites."
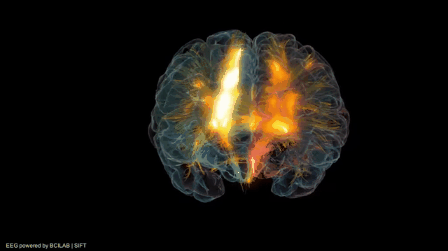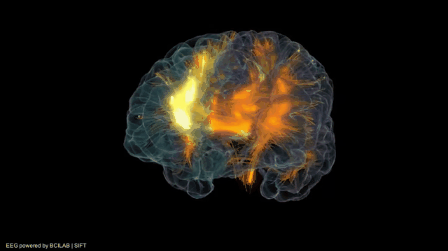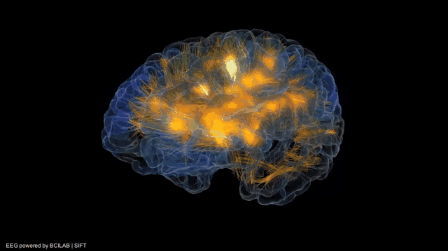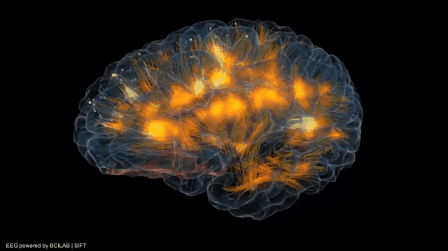
"A neuron does nothing unless the collective influence of all its inputs reaches a threshold level. Whenever that threshold level is reached, the neuron produces a full-strength output in the form of a narrow pulse that proceeds from the cell body, down the axon, and into the axon's branches. Whenever this happens, the neuron is said to fire. Because a neuron either fires or does nothing, it is said to be an all-or-none device.
Axons influence dendrites over narrow gaps called synapses. Stimulation at some synapses encourages neurons to fire. Stimulation at others discourages neurons from firing. There is mounting evidence that learning takes place in the vicinity of synapses and has something to do with the degree to which synapses translate the pulse traveling down one neuron's axon into excitation or inhibition of the next neuron.
The number of neurons in the human brain is staggering. Current estimates suggest there may be on the order of 1011 neurons per person. If the number of neurons is staggering, the number of synapses must be toppling. In the cerebellum--that part of the brain that is crucial to motor coordination--a single neuron may receive inputs from as many as 105 synapses."
Artificial Intelligence, Patrick Winston
Winston does an excellent job further describing how we can mimic biology in our Neural Network model...
"Simulated neural nets typically consist of simulated neurons. The simulated neuron is viewed as a node connected to other nodes via links that correspond to axon-synapse-dendrite connections."
Artificial Intelligence, Patrick Winston
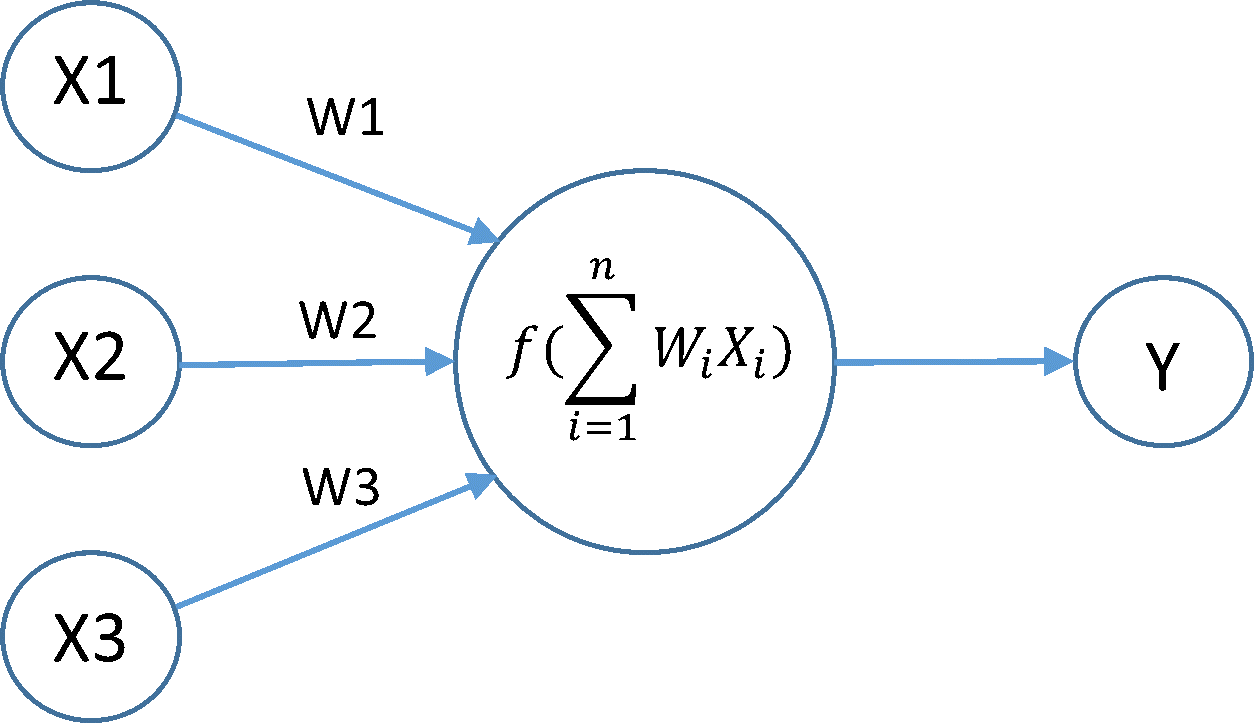
In the Diagram above, X is our input (in this case not a neuron!), W is a synaptic weight, the function is our neuron and its respective activation function, and Y is the output neuron.
"Each link or (W) in the diagram is associated with a weight. Like a synapse, that weight determines the nature and strength of one neuron's influence on another. More specifically, one node's influence on another is the product of the influencing neuron's output value times the connecting link's weight. Thus, a large positive weight corresponds to strong excitation, and a small negative weight corresponds to weak inhibition.
Each node combines the seperate influences received on its input links into an overall influence using an activation function. One simple activation function simply passes the sum of the input values through a threshold function to determine the node's output. The output of each node is either 0 or 1 depending on whether the sum of the inputs is below or above the threshold value used by the node's threshold function.
Now you can understand what is modeled in these simplified neurons: the weights model synaptic properties; the adder models the influence-combining capability of the dendrites; and comparison with a threshold models the all-or-none characteristic imposed by electrochemical mechanisms in the cell body."
Artificial Intelligence, Patrick Winston
Now is a good time to introduce the example presented in Stephen Welch's lectures.
"Suppose we recorded how many hours we slept, and how many hours we studied and the score we received on a test the next day. We can use artificial neural networks to predict a score based on hourse slept, and hours studying."
Data
| X (Hrs Sleep, Hrs Study) | y (Test Score) |
| (3, 5) | (75) |
| (5, 1) | (82) |
| (10, 2) | (93) |
| (8, 3) | (?) |
If you are not using the Ipython Notebook environment, then the first thing we have to do to program our Neural Network is import the necessary dependencies.
import time #Algorithm Comparison
import numpy as np #Matrix Multiplication
import matplotlib as mpl #Graphs
import matplotlib.pyplot as plt #Graphs
from scipy import optimize #BFGS Algorithm
from mpl_toolkits.mplot3d import Axes3D #Graphs
import matplotlib.colors as colors #Heat Maps
import matplotlib.cm as cmx #Heat Maps
Now lets model our data.
X = (Hours Sleeping, Hours Studying)
X = np.array(([3,5], [5,1], [10,2]), dtype=float)
y = (Test Score)
y = np.array(([75], [82], [93]), dtype=float)
"The problem above is referred to as a supervised regression problem. It is supervised because we have inputs and outputs, and it is a regression because we are predicting test score, which is a continuous function." -Stephen Welch
Architecture
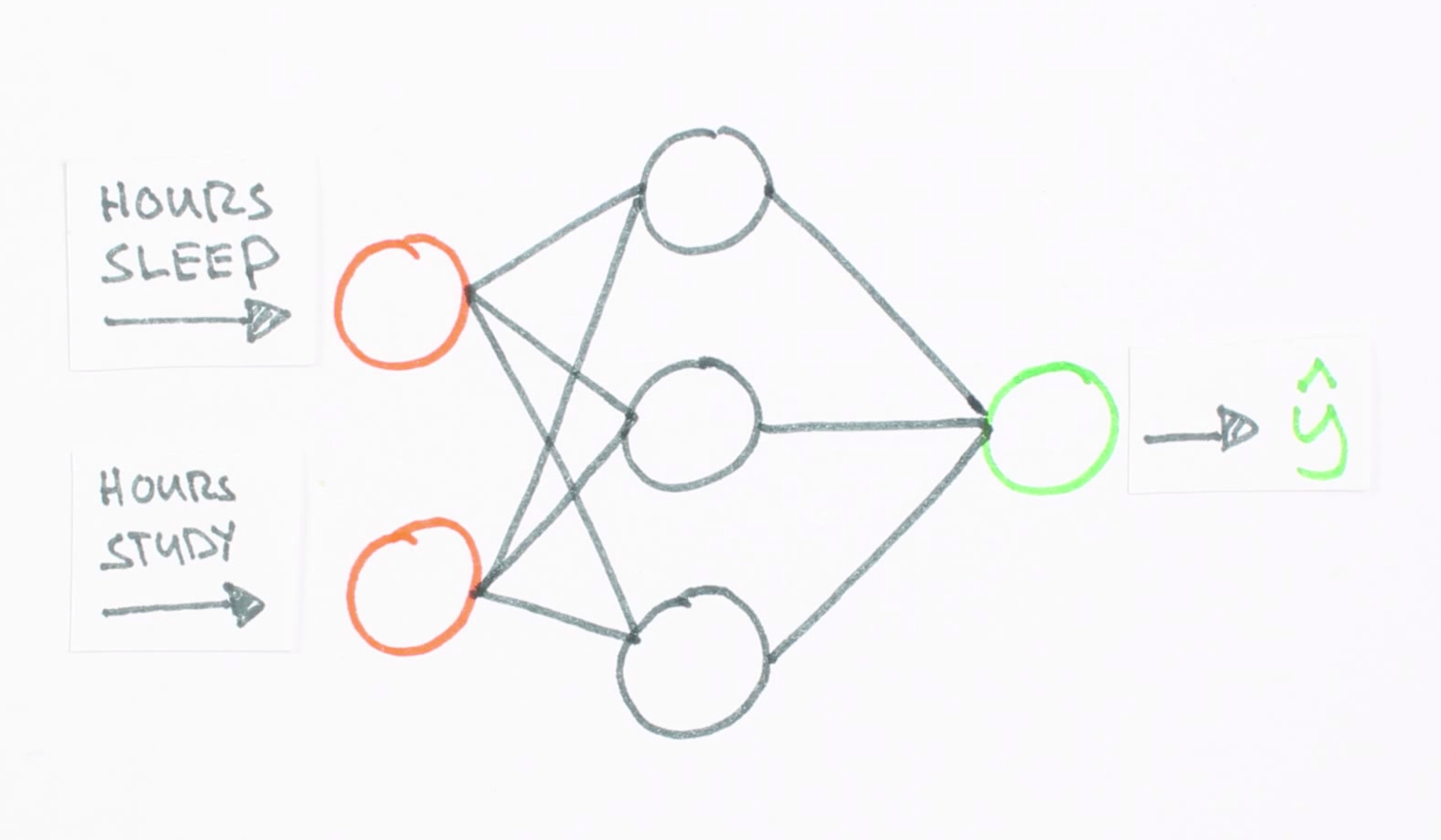
Source: Neural Networks Demystified, Stephen C Welch
Our neural network is comprised of two abstract objects, neurons and synapses.

Neurons: a neuron adds up all the outputs from its synapses and applies an activation function.
1. Z = X1 + X2 + X3
2. a = 1 / (1 + e-Z) Using a sigmoid activation allows our neural network to model complex non-linear patterns.

Synapses: a synapse takes a value from it's input, multiplies it by a synaptic Weight, then outputs the results.
1. X*W
This model for a perceptron is quite good so far, but our data needs to reflect the model before we can begin forward propagation. We will fix this problem by normalizing our data. We will take advantage of the fact that our test scores are out of 100 to normalize y, and we will simply divide X by the maximum value.
print('\n')
print('Artificial Neural Network')
print('\n')
print('Input Data')
print(X)
print('\n')
print('Output Data')
print(y)
#Normalize Data
print('\n')
print('Normalized Input Data')
X = X/np.amax(X, axis=0)
print(X)
print('\n')
print('Normalized Output Data')
y = y/100 #Max test score is 100
print(y)
This completes the setup of our Data and Architecture. Next we will begin Forward Propagation.
Forward Propagation
We know the mechanics of neurons and synapses now, so lets combine that knowledge with our current model as Welch does in Neural Networks Demystified.
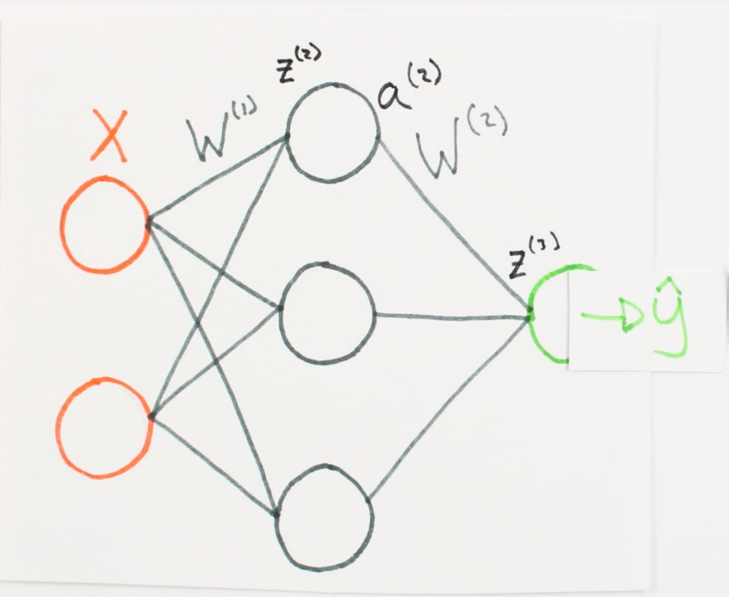
Forward Propagation is going to involve five steps.
X = np.array(([3,5], [5,1], [10,2]), dtype=float)
y = np.array(([75], [82], [93]), dtype=float)
X
y
1. Normalize Data
X = X/np.amax(X, axis=0)
y = y/100 #Max test score is 100
X
y
2. Multiply our input matrix X by our first layer synaptic weights (W1) to find Z2.
For now, lets just give W1 and W2 random values.
W1 = np.random.randn(2, 3)
W2 = np.random.randn(3,1)
W1
W2
We can take advantage of numpy's dot method to multiply our matrices X and W1 to find Z2
z2 = np.dot(X, W1)
z2
3. Apply our sigmoid activation function a2 = 1 / (1 + e-Z)
def sigmoid(z):
return 1/(1+np.exp(-z))
Before we go further we should test our sigmoid function.
testInput = np.arange(-6,6,0.01)
plot(testInput, sigmoid(testInput), linewidth= 2)
grid(1)
Looks Good!
a2 = sigmoid(z2)
a2
4. Multiply a2 by our second layer synaptic weights (W2) to find Z3.
z3 = np.dot(z2, W2)
z3
5. Apply our sigmoid activation function to Z3 to find yHat, or in other words, our predicted output!
yHat = sigmoid(z3)
yHat
And there you have it! We have successfully predicted Test Scores given actual "real-life" examples of combinations of sleep and study. Why are our values so poor?
We have run into our first interesting problem in artificial intelligence. Although we have successfully modeled the functionality of a neuron and weight, our function does not give us good predictions. The problem is that we have not trained our network. Much like if we were to present the 45 degree triangle example to a baby, our neural network object is not smart enough to give good predictions or "imagine" a good answer. The solution is to train our network, but we have a few things to do first.
Basic Feed Forward (Forward Propagating) Neural Network
#Neural Network
class NeuralNetwork(object):
def __init__(self):
#Hyperparameters
self.inputLayerSize = 2
self.outputLayerSize = 1
self.hiddenLayerSize = 3
#Synaptic Weights
self.W1 = np.random.randn(self.inputLayerSize, self.hiddenLayerSize)
self.W2 = np.random.randn(self.hiddenLayerSize, self.outputLayerSize)
def forward(self, X):
#Propagate inputs feed forward through our network
self.z2 = np.dot(X, self.W1)
self.a2 = self.sigmoid(self.z2)
self.z3 = np.dot(self.a2, self.W2)
yHat = self.sigmoid(self.z3)
return yHat
def sigmoid(self, z):
#Apply sigmoid activation function
return 1/(1+np.exp(-z))
NN = NeuralNetwork()
yHat = NN.forward(X)
yHat
#Compare estimate, yHat, to actually score
bar([0,1,2], y, width = 0.35, alpha=0.8)
bar([0.35,1.35,2.35],yHat, width = 0.35, color='r', alpha=0.8)
grid(1)
legend(['y', 'yHat'])
To reiterate, our network is not making very good predictions. We need to fix this problem by minimizing the amount of error between our real life test values, y, and our Neural Network's predictions for y in regards to the values for the synaptic weights, yHat. We will explore the solution to this problem, Gradient Descent.
Gradient Descent
Humans do not just think feed forward. Although feed forward networks are good for making decisions, and the perceptron model can get as advanced as NAND gates (as some research into circuits will show), they do not correct themselves when they make incorrect decisions. This is the problem with our network.
Imagine it is wintertime, and you need to drive to class in an old car. Before your car can run you must warm up the engine and the cold oil, allowing it to disperse around your car's inner mechanics. Each time you drive to class you are going to try a random value for time to warm up your car. The synaptic weight you apply to that time for it's quantification of success would be similar to the weights in our scenario. Eventually, we will devise a way to test some random values, find the best random value, and simulate learning. Right now, using our neural network, sometimes we would choose the right value for time, and sometimes we would not, and we would not account for error. The goal of this week's journal is to find a way to quantify this error. We will visit how to train the network in Week 4's journal.
Our data is dependent upon the input values X and y, and the synaptic weights. When we run our network feed forward on X, we can use the predicted results, yHat and y to analyze the error, or "cost" of our values for W. This function can be expressed as J=(y-yHat), where J is the cost. This function is good, but let's modify it somewhat. Later in this journal series, we will analyze why we chose this cost function, but for now, let us set J=1/2(y-yHat)2. Additionally, we have many synaptic weights, and we need to test all 9 of our values for W, so our function becomes: J = Σ1/2(y-yHat)2.
As Stephen Welch states, "When someone refers to training a network, what they really mean is minimizing a cost function."
Now that we know our goal, we need to simply adjust values of W to minimize our cost function. How long does this take however? Let's explore that question using Python's time class on just one synaptic weight for 1000 random values for W.
import time
weightsToTry = np.linspace(-5,5,1000)
costs = np.zeros(1000)
startTime = time.clock()
for i in range(1000):
NN.W1[0,0] = weightsToTry[i]
yHat = NN.forward(X)
costs[i] = 0.5*sum((y-yHat)**2)
endTime = time.clock()
timeElapsed = endTime-startTime
timeElapsed
If we entertain the idea that the above result of about .3 seconds is reasonable, we can just plot our weights and the cost and pick the smallest value.
plot(weightsToTry, costs)
grid(1)
ylabel('Cost')
xlabel('Weight')
We have indeed successfully minimized our cost function in terms of one synaptic weight, however, lets see how long it takes to simply try 1000 random values for 2 weights...
weightsToTry = np.linspace(-5,5,1000)
costs = np.zeros((1000, 1000))
startTime = time.clock()
for i in range(1000):
for j in range(1000):
NN.W1[0,0] = weightsToTry[i]
NN.W1[0,1] = weightsToTry[j]
yHat = NN.forward(X)
costs[i, j] = 0.5*sum((y-yHat)**2)
endTime = time.clock()
timeElapsed = endTime-startTime
timeElapsed
Ouch, that is starting to take some time. This is due to dimensionality, as demonstrated by the calculation below which shows how long it would take to check 9 weights for 1000 random values. The answer is more than the time since the birth of the universe, so let's try and find a better way to minimize our cost function.
0.04*(1000**(9-1))/(3600*24*365)
So far, our network takes some normalized input matrix, X and multiplies it by our first layer of synaptic weights W1 to get matrix Z2. Next, this matrix is multiplied by our activation function, f(Z2) to get matrix a2. a2 is multiplied by the second layer of synaptic weights W2 to find Z3, and finally we apply our activation function to Z3 to find yHat, our predicted test scores.
Equations
Additionally, we found that if we change the values for the weights, it has an effect on the output yHat. More specifically, if we create an equation for the difference between yHat and y, or a cost function J, we can quantify how wrong our predictions are and adjust the synaptic weights accordingly. We chose this cost function to be J = Σ(1/2(y - yHat)2). By choosing the correct combination of synaptic weights we can minimize the cost function and ensure we are making the best possible predictions. Now our list of equations becomes...
Equations
Let's rewrite our equations in terms of our cost function, J.
J = Σ 1/2( y - f( f( XW(1) ) W(2) ) )2
We have no control over our input data, as that is a model of real life information and if manipulated, would manipulate our results. What we do have to work with are our weights. If we can find how J changes in respect to W(1) and W(2), or in other words the partial derivative of J in terms of W, or ∂J/∂W(1) and ∂J/∂W(2), we can find where our function is going downhill.
We can increase or decrease W(1) and W(2) and observe it's effect on our partial derivatives. If they are increasing we know that the rate of change is positive, and similarly if they are negative, the rate of change is decreasing. If we iteratively repeat this process until the partial derivatives stop decreasing, then we have reached the minimum of our cost function and have completed our objective; or in other words have found a combination of synaptic weights that minimizes the cost.
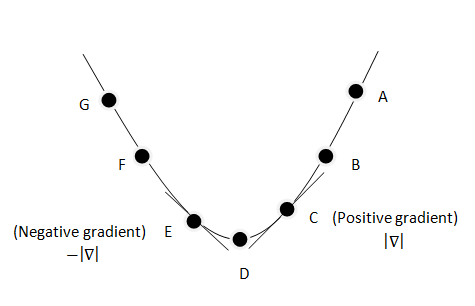
This is the core idea of Gradient Descent. We have a function and we find where the slope of that function is at a minimum, or zero. This value corresponds to the best possible synaptic weights for that synapse. The next step in our Neural Network is Backpropagation, so now we will need to derive values for ∂J/∂W(1) and ∂J/∂W(2)
*It is important to now bring up why we chose our cost function to be the sum of squared errors. If you examine the graph above, it is very clear to see where the minimum is, however observe the graph below.
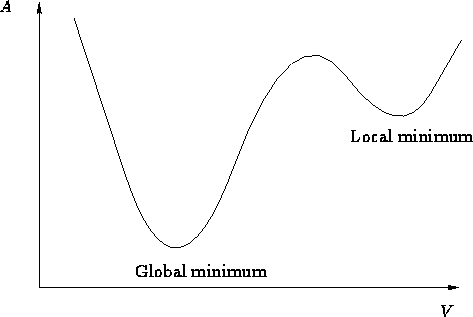
As you can see, there is still a possibility that gradient descent will find a local minimum rather than the necessary global minimum. Luckily for us, the sum of squared errors function is naturally convex, and is naturally convex for really high dimensions as well, which is good for us considering our optimization space is 9 dimensional!
Backpropagation
The goal of Backpropagation is to find a function that we can program for our partial derivatives ∂J/∂W(1) and ∂J/∂W(2). The reason we are finding two partial derivatives is because we have two layers of synaptic weights that determine our data flow. If one needed to modify their network in the future, they could simply calculate a partial derivative for each layer of weights.
The shape of our synaptic weight matrices determine the shape of the corresponding partial derivative matrices. Let's verify these shapes using numpy's shape function.
inputLayerSize = 2
outputLayerSize = 1
hiddenLayerSize = 3
W1 = np.random.randn(inputLayerSize, hiddenLayerSize)
W1
W2 = np.random.randn(hiddenLayerSize, outputLayerSize)
W2
W1.shape
W2.shape
So ∂J/∂W(1) will have shape (2,3), and ∂J/∂W(2) will have shape (3,1).
Our cost function so far is J = Σ 1/2( y - f( f( XW(1) ) W(2) ) )2.
Deriving ∂J/∂W(2)
Let's work on ∂J/∂W(2) first.
You may recall from your calculus classes that we have a nifty rule called the sum rule which states "the derivative of the sum is equal to the sum of the derivatives. We are going to take advantage of this property and calculate our gradients one by one, batch style, one by one and then sum them instead of accounting for the summation in our equations. This allows us to rewrite our partial derivative as...
The second thing you may recall from your calculus classes is the power rule. Using the power rule we multiply the 1/2 by our exponent 2, and our partial derivative becomes...
The THIRD thing you may recall from your calculus classes is the powerful chain rule. The chain rule is somewhat more complicated than the power or summation rule of differentiation.
Chain Rule, f of g prime is equal to g prime times f prime of g.
ex.
d/dx( 2x + 3x3 )2 = 2( 2x + 3x3 )( 2 + 9x2 )
Another way to express the chain rule is as the product of derivatives,
dZ/dX = dZ/dY * dY/dX
This will be really helpful later.
In our function, the derivative of y is simply zero.
yHat on the other hand, changes with respect to W2, so using the chain rule and multiplying by the partial derivative of yHat, our partial derivative becomes...
We need to put yHat in terms of W2. We know from our equations that yHat = 1/1+e-Z(3)</sup>or, yHat = f(Z(3).
From the chain rule, let's use the products of derivatives and rewrite our equation in terms of f(Z(3)).
To find ∂yHat/∂Z(3) (our second term from the products of derivatives), we need to differentiate our activaction function f(z).
We can now replace ∂yHat/∂Z(3) with f'(Z(3))
Now is a good time to switch back to our neural network and define a method to calculate sigmoid prime.
#Sigmoid Function
def sigmoid(z):
#Apply sigmoid activation function to scalar, vector, or matrix
return 1/(1+np.exp(-z))
#Sigmoid' Function
def sigmoidPrime(z):
return np.exp(-z)/((1+np.exp(-z))**2)
If we implemented our derivative correctly, our sigmoidPrime function should be largest where the sigmoid function is the steepest.
testValues = np.arange(-5,5,0.01)
plot(testValues, sigmoid(testValues), linewidth=2)
plot(testValues, sigmoidPrime(testValues), linewidth=2)
grid(1)
legend(['sigmoid', 'sigmoidPrime'])
Looks Good!
The final term we have to differentiate is ∂Z(3)/∂W(2).
We know from equation 3 that Z is dependent on a(2) and the weights from the second layer.
If we rewrite our equation as a(2) = Z(3) / W(2), we can see that there is a linear relationship between Z and W, where a is the slope.
Stephen Welch makes a great point in his tutorial on Neural Networks about what is actually happening here.
"Another way to think about what our calculus is doing here is that it is backpropagating the error to each weight. By multiplying by the activity on each synapse, the weights that contribute more to the overall error will have larger activations, yield larger ∂J/∂W(2) values, and will be changed more when we perform gradient descent!
yminusyHat = np.array((["-y-yHat"],["-y-yHat"],["-y-yHat"]))
Z3 = np.array((["f'(z3)"],["f'(z3)"],["f'(z3)"]))
delta3 = np.array((["delta3"],["delta3"],["delta3"]))
yminusyHat
The value of -(y-yHat) * f'(Z(3)) is also referred to as the backpropagating error, δ(3)
Z3
delta3
Deriving ∂J/∂W(1)
As you may recall, our function for ∂J/∂W(1) is...
We can start our derivation the same way as for ∂J/∂W(2) = 1/2( y - yHat )2 by using the power rule to get,
Next we apply the chain rule,
We can differentiate ∂yHat/∂Z(3) the same way as for ∂J/∂W(2),
To find the derivative across our synapses, we use the product of derivatives to get,
This is different than our calculation for ∂J/∂W(2), because rather than a(2) being our slope, it is rather W(1) because we are trying to find the slope of ∂Z(3)/∂a(2).
Therefore, the next step is to multiply δ(3) by W(2)T
The next step is to derive ∂a(2)/∂W(1)
From deriving ∂J/∂W(2), we know that,
This makes our partial derivative,
There is a simple linear relationship between Z(2) and W(1), from equation 1. Z(2) = XW(1), where the slope is simply X. Now we have all the pieces of our partial derivative!
Our full list of equations becomes...
Equations
Now let's write some code for our partial derivatives. We will refer to ∂J/∂W(1) and DJDW1, and ∂J/∂W(2) as DJDW2.
∂J/∂W(1) = XT δ(3) ( W(2) )T f '( Z(2) ). We can represent this in python as,
dJdW1 = np.dot(X.T, delta2)
delta2 = np.dot(delta3, self.W2.T)*self.sigmoidPrime(self.z2)
dJdW2 = np.dot(self.a2.T, delta3)
delta3 = np.multiply(-(y-self.yHat), self.sigmoidPrime(self.z3))
The full Neural Network Class with changes to the cost function...
# Whole Class with additions:
class Neural_Network(object):
def __init__(self):
#Define Hyperparameters
self.inputLayerSize = 2
self.outputLayerSize = 1
self.hiddenLayerSize = 3
#Weights (parameters)
self.W1 = np.random.randn(self.inputLayerSize,self.hiddenLayerSize)
self.W2 = np.random.randn(self.hiddenLayerSize,self.outputLayerSize)
def forward(self, X):
#Propogate inputs though network
self.z2 = np.dot(X, self.W1)
self.a2 = self.sigmoid(self.z2)
self.z3 = np.dot(self.a2, self.W2)
yHat = self.sigmoid(self.z3)
return yHat
def sigmoid(self, z):
#Apply sigmoid activation function to scalar, vector, or matrix
return 1/(1+np.exp(-z))
def sigmoidPrime(self,z):
#Gradient of sigmoid
return np.exp(-z)/((1+np.exp(-z))**2)
def costFunction(self, X, y):
#Compute cost for given X,y, use weights already stored in class.
self.yHat = self.forward(X)
J = 0.5*sum((y-self.yHat)**2)
return J
def costFunctionPrime(self, X, y):
#Compute derivative with respect to W and W2 for a given X and y:
self.yHat = self.forward(X)
delta3 = np.multiply(-(y-self.yHat), self.sigmoidPrime(self.z3))
dJdW2 = np.dot(self.a2.T, delta3)
delta2 = np.dot(delta3, self.W2.T)*self.sigmoidPrime(self.z2)
dJdW1 = np.dot(X.T, delta2)
return dJdW1, dJdW2
"We can now find DJDW, which will tell us which way is downhill in our 9 dimensional optimization space."
X = np.array(([3,5], [5,1], [10,2]), dtype=float)
y = np.array(([75], [82], [93]), dtype=float)
X = X/np.amax(X, axis=0)
y = y/100 #Max test score is 100
NN = Neural_Network()
cost1 = NN.costFunction(X,y)
dJdW1, dJdW2 = NN.costFunctionPrime(X,y)
dJdW1
dJdW2
"If we move this way by adding a scalar times our derivative to all of our weights, our cost will increase."
scalar = 3
NN.W1 = NN.W1 + scalar*dJdW1
NN.W2 = NN.W2 + scalar*dJdW2
cost2 = NN.costFunction(X,y)
cost1
cost2
"If we do the opposite, subtract our gradient from our weights, we will reduce our cost."
dJdW1, dJdW2 = NN.costFunctionPrime(X,y)
NN.W1 = NN.W1 - scalar*dJdW1
NN.W2 = NN.W2 - scalar*dJdW2
cost3 = NN.costFunction(X, y)
cost2
cost3
Numerical Gradient Checking
Now that we found the rate of change of our cost function, we need a way to check for errors in our code. If we are going to modify our network in the future such as use a different cost function or optimization method, we need a way to make sure our gradients are still being calculated correctly. One way we can do this is by using the definition of the derivative to error check our gradients.
Definition of the derivative:
f '(x) = limΔx→0 f( x + Δx ) - f( x ) / Δx
The definition of the derivative is really just a glorified slope formula, where the top part is the change in y, and the bottom is Δx.
By modifying the formula for the derivative somewhat, we can use it to test our gradients. If we use a reasonably small value for delta, or in our case epsilon, we can find the values around our gradient and compare them to the actual derivative.
def f(x):
return x**2
epsilon = 1e-4
x = 1.5
numericalGradient = (f(x+epsilon)- f(x-epsilon))/(2*epsilon)
numericalGradient, 2*x
Looks close enough for me!
Stephen Welch wrote a great method for iteratively calculating the numerical gradient for each of the gradients in our network, let's test this method.
def computeNumericalGradient(N, X, y):
paramsInitial = N.getParams()
numgrad = np.zeros(paramsInitial.shape)
perturb = np.zeros(paramsInitial.shape)
e = 1e-4
for p in range(len(paramsInitial)):
#Set perturbation vector
perturb[p] = e
N.setParams(paramsInitial + perturb)
loss2 = N.costFunction(X, y)
N.setParams(paramsInitial - perturb)
loss1 = N.costFunction(X, y)
#Compute Numerical Gradient
numgrad[p] = (loss2 - loss1) / (2*e)
#Return the value we changed to zero:
perturb[p] = 0
#Return Params to original value:
N.setParams(paramsInitial)
return numgrad
class Neural_Network(object):
def __init__(self):
#Define Hyperparameters
self.inputLayerSize = 2
self.outputLayerSize = 1
self.hiddenLayerSize = 3
#Weights (parameters)
self.W1 = np.random.randn(self.inputLayerSize,self.hiddenLayerSize)
self.W2 = np.random.randn(self.hiddenLayerSize,self.outputLayerSize)
def forward(self, X):
#Propogate inputs though network
self.z2 = np.dot(X, self.W1)
self.a2 = self.sigmoid(self.z2)
self.z3 = np.dot(self.a2, self.W2)
yHat = self.sigmoid(self.z3)
return yHat
def sigmoid(self, z):
#Apply sigmoid activation function to scalar, vector, or matrix
return 1/(1+np.exp(-z))
def sigmoidPrime(self,z):
#Gradient of sigmoid
return np.exp(-z)/((1+np.exp(-z))**2)
def costFunction(self, X, y):
#Compute cost for given X,y, use weights already stored in class.
self.yHat = self.forward(X)
J = 0.5*sum((y-self.yHat)**2)
return J
def costFunctionPrime(self, X, y):
#Compute derivative with respect to W and W2 for a given X and y:
self.yHat = self.forward(X)
delta3 = np.multiply(-(y-self.yHat), self.sigmoidPrime(self.z3))
dJdW2 = np.dot(self.a2.T, delta3)
delta2 = np.dot(delta3, self.W2.T)*self.sigmoidPrime(self.z2)
dJdW1 = np.dot(X.T, delta2)
return dJdW1, dJdW2
#Helper Functions for interacting with other classes:
def getParams(self):
#Get W1 and W2 unrolled into vector:
params = np.concatenate((self.W1.ravel(), self.W2.ravel()))
return params
def setParams(self, params):
#Set W1 and W2 using single paramater vector.
W1_start = 0
W1_end = self.hiddenLayerSize * self.inputLayerSize
self.W1 = np.reshape(params[W1_start:W1_end], (self.inputLayerSize , self.hiddenLayerSize))
W2_end = W1_end + self.hiddenLayerSize*self.outputLayerSize
self.W2 = np.reshape(params[W1_end:W2_end], (self.hiddenLayerSize, self.outputLayerSize))
def computeGradients(self, X, y):
dJdW1, dJdW2 = self.costFunctionPrime(X, y)
return np.concatenate((dJdW1.ravel(), dJdW2.ravel()))
NN = Neural_Network()
X = np.array(([3,5], [5,1], [10,2]), dtype=float)
y = np.array(([75], [82], [93]), dtype=float)
X = X/np.amax(X, axis=0)
y = y/100 #Max test score is 100
numgrad = computeNumericalGradient(NN, X, y)
numgrad
grad = NN.computeGradients(X,y)
grad
By using numpy's built in norm method, we can calculate the difference between our calculations for the gradient, and the numerical gradient.
norm(grad-numgrad)/norm(grad+numgrad)
If this value is extremely small, then we know our gradients are being calculated correctly.
Training
There are many ways to optimize a neural network. Although Gradient Descent performs well, it still has it's limitations in the way that it could get stuck in a local minimum. Another way we can make sure our gradients and cost function are correct is to implement one of the optimization algorithms contained in the scipy package called the BFGS algorithm. This algorithm takes in a function, with the input and output data, and returns a cost and the gradients. Stephen Welch includes a wrapper function in the trainer method to implement this behavior in our neural network as seen below.
import scipy as sp
import numpy as np
from scipy import optimize
class Neural_Network(object):
def __init__(self):
#Define Hyperparameters
self.inputLayerSize = 2
self.outputLayerSize = 1
self.hiddenLayerSize = 3
#Weights (parameters)
self.W1 = np.random.randn(self.inputLayerSize,self.hiddenLayerSize)
self.W2 = np.random.randn(self.hiddenLayerSize,self.outputLayerSize)
def forward(self, X):
#Propogate inputs though network
self.z2 = np.dot(X, self.W1)
self.a2 = self.sigmoid(self.z2)
self.z3 = np.dot(self.a2, self.W2)
yHat = self.sigmoid(self.z3)
return yHat
def sigmoid(self, z):
#Apply sigmoid activation function to scalar, vector, or matrix
return 1/(1+np.exp(-z))
def sigmoidPrime(self,z):
#Gradient of sigmoid
return np.exp(-z)/((1+np.exp(-z))**2)
def costFunction(self, X, y):
#Compute cost for given X,y, use weights already stored in class.
self.yHat = self.forward(X)
J = 0.5*sum((y-self.yHat)**2)
return J
def costFunctionPrime(self, X, y):
#Compute derivative with respect to W and W2 for a given X and y:
self.yHat = self.forward(X)
delta3 = np.multiply(-(y-self.yHat), self.sigmoidPrime(self.z3))
dJdW2 = np.dot(self.a2.T, delta3)
delta2 = np.dot(delta3, self.W2.T)*self.sigmoidPrime(self.z2)
dJdW1 = np.dot(X.T, delta2)
return dJdW1, dJdW2
#Helper Functions for interacting with other classes:
def getParams(self):
#Get W1 and W2 unrolled into vector:
params = np.concatenate((self.W1.ravel(), self.W2.ravel()))
return params
def setParams(self, params):
#Set W1 and W2 using single paramater vector.
W1_start = 0
W1_end = self.hiddenLayerSize * self.inputLayerSize
self.W1 = np.reshape(params[W1_start:W1_end], (self.inputLayerSize , self.hiddenLayerSize))
W2_end = W1_end + self.hiddenLayerSize*self.outputLayerSize
self.W2 = np.reshape(params[W1_end:W2_end], (self.hiddenLayerSize, self.outputLayerSize))
def computeGradients(self, X, y):
dJdW1, dJdW2 = self.costFunctionPrime(X, y)
return np.concatenate((dJdW1.ravel(), dJdW2.ravel()))
def computeNumericalGradient(N, X, y):
paramsInitial = N.getParams()
numgrad = np.zeros(paramsInitial.shape)
perturb = np.zeros(paramsInitial.shape)
e = 1e-4
for p in range(len(paramsInitial)):
#Set perturbation vector
perturb[p] = e
N.setParams(paramsInitial + perturb)
loss2 = N.costFunction(X, y)
N.setParams(paramsInitial - perturb)
loss1 = N.costFunction(X, y)
#Compute Numerical Gradient
numgrad[p] = (loss2 - loss1) / (2*e)
#Return the value we changed to zero:
perturb[p] = 0
#Return Params to original value:
N.setParams(paramsInitial)
return numgrad
class trainer(object):
def __init__(self, N):
#Make Local reference to network:
self.N = N
def callbackF(self, params):
self.N.setParams(params)
self.J.append(self.N.costFunction(self.X, self.y))
def costFunctionWrapper(self, params, X, y):
self.N.setParams(params)
cost = self.N.costFunction(X, y)
grad = self.N.computeGradients(X,y)
return cost, grad
def train(self, X, y):
#Make an internal variable for the callback function:
self.X = X
self.y = y
#Make empty list to store costs:
self.J = []
params0 = self.N.getParams()
options = {'maxiter': 200, 'disp' : True}
_res = sp.optimize.minimize(self.costFunctionWrapper, params0, jac=True, method='BFGS', \
args=(X, y), options=options, callback=self.callbackF)
self.N.setParams(_res.x)
self.optimizationResults = _res
After our network is trained, the trainer method replaces our random values for W with the trained values.
NN = Neural_Network()
X = np.array(([3,5], [5,1], [10,2]), dtype=float)
y = np.array(([75], [82], [93]), dtype=float)
X = X/np.amax(X, axis=0)
y = y/100 #Max test score is 100
T = trainer(NN)
T.train(X,y)
If we plot the cost against the number of iterations it takes to train the network, we can see the function decrease monotonically each time it trains the network with new gradients and costs. Additionally, we can see from the training output that it only took us 37 evaluations to minimize the cost function.
plot(T.J)
grid(1)
xlabel('Iterations')
ylabel('Cost')
As another way to error check our code, we can evaluate our gradients at our solution and expect to see very small values.
NN.costFunctionPrime(X,y)
At this point we have trained our network to predict an accurate score, which we can test by running our new trained data through the feed forward method.
NN.forward(X)
y
As you can see, the values are very close to one another, validating our neural network! Now let's examine our input space for many values of sleeping and studying.
#Test network for various combinations of sleep/study:
hoursSleep = np.linspace(0, 10, 100)
hoursStudy = np.linspace(0, 5, 100)
#Normalize data (same way training data way normalized)
hoursSleepNorm = hoursSleep/10.
hoursStudyNorm = hoursStudy/5.
#Create 2-d versions of input for plotting
a, b = np.meshgrid(hoursSleepNorm, hoursStudyNorm)
#Join into a single input matrix:
allInputs = np.zeros((a.size, 2))
allInputs[:, 0] = a.ravel()
allInputs[:, 1] = b.ravel()
allOutputs = NN.forward(allInputs)
#Contour Plot:
yy = np.dot(hoursStudy.reshape(100,1), np.ones((1,100)))
xx = np.dot(hoursSleep.reshape(100,1), np.ones((1,100))).T
CS = contour(xx,yy,100*allOutputs.reshape(100, 100))
clabel(CS, inline=1, fontsize=10)
xlabel('Hours Sleep')
ylabel('Hours Study')
#3D plot:
##Uncomment to plot out-of-notebook (you'll be able to rotate)
#%matplotlib qt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.gca(projection='3d')
surf = ax.plot_surface(xx, yy, 100*allOutputs.reshape(100, 100), \
cmap=cm.jet)
ax.set_xlabel('Hours Sleep')
ax.set_ylabel('Hours Study')
ax.set_zlabel('Test Score')
Our results look quite reasonable, and it seems like sleep actually had a greater impact on test score than hours studying which is interesting. At this point it may seem like we have successfully trained our network, but we made one of the most common mistakes in Neural Networks, we overfit our data.
Overfitting, Testing, and Regularization
Let's modify our data a bit to make our overfitting mistake more apparent.
NN = Neural_Network()
# X = (hours sleeping, hours studying), y = Score on test
X = np.array(([3,5], [5,1], [10,2], [6,1.5]), dtype=float)
y = np.array(([75], [82], [93], [70]), dtype=float)
#Plot projections of our new data:
fig = figure(0,(8,3))
subplot(1,2,1)
scatter(X[:,0], y)
grid(1)
xlabel('Hours Sleeping')
ylabel('Test Score')
subplot(1,2,2)
scatter(X[:,1], y)
grid(1)
xlabel('Hours Studying')
ylabel('Test Score')
#Normalize
X = X/np.amax(X, axis=0)
y = y/100 #Max test score is 100
#Train network with new data:
T = trainer(NN)
T.train(X,y)
#Plot cost during training:
plot(T.J)
grid(1)
xlabel('Iterations')
ylabel('Cost')
#Test network for various combinations of sleep/study:
hoursSleep = linspace(0, 10, 100)
hoursStudy = linspace(0, 5, 100)
#Normalize data (same way training data way normalized)
hoursSleepNorm = hoursSleep/10.
hoursStudyNorm = hoursStudy/5.
#Create 2-d versions of input for plotting
a, b = meshgrid(hoursSleepNorm, hoursStudyNorm)
#Join into a single input matrix:
allInputs = np.zeros((a.size, 2))
allInputs[:, 0] = a.ravel()
allInputs[:, 1] = b.ravel()
allOutputs = NN.forward(allInputs)
#Contour Plot:
yy = np.dot(hoursStudy.reshape(100,1), np.ones((1,100)))
xx = np.dot(hoursSleep.reshape(100,1), np.ones((1,100))).T
CS = contour(xx,yy,100*allOutputs.reshape(100, 100))
clabel(CS, inline=1, fontsize=10)
xlabel('Hours Sleep')
ylabel('Hours Study')
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.gca(projection='3d')
#Scatter training examples:
ax.scatter(10*X[:,0], 5*X[:,1], 100*y, c='k', alpha = 1, s=30)
surf = ax.plot_surface(xx, yy, 100*allOutputs.reshape(100, 100), \
cmap=cm.jet, alpha = 0.5)
ax.set_xlabel('Hours Sleep')
ax.set_ylabel('Hours Study')
ax.set_zlabel('Test Score')
If we reexamine our solution space, we see how our model is overfitting the data. Our data is too closely fit to our input data, and this makes our network no longer reflective of the real world. One way to fix this problem is to have more examples for our network. For each weight, there is a general rule of thumb that you should have ten test cases. In our case that would mean we would need 90 sets of data for sleeping, studying, and test score. Since we do not have that much data we will have to use another strategy to correctly fit our network.
Let's split our data into training and testing data to find the exact point where overfitting begins.
#Training Data:
trainX = np.array(([3,5], [5,1], [10,2], [6,1.5]), dtype=float)
trainY = np.array(([75], [82], [93], [70]), dtype=float)
#Testing Data:
testX = np.array(([4, 5.5], [4.5,1], [9,2.5], [6, 2]), dtype=float)
testY = np.array(([70], [89], [85], [75]), dtype=float)
#Normalize:
trainX = trainX/np.amax(trainX, axis=0)
trainY = trainY/100 #Max test score is 100
#Normalize by max of training data:
testX = testX/np.amax(trainX, axis=0)
testY = testY/100 #Max test score is 100
#Need to modify trainer class a bit to check testing error during training:
class trainer(object):
def __init__(self, N):
#Make Local reference to network:
self.N = N
def callbackF(self, params):
self.N.setParams(params)
self.J.append(self.N.costFunction(self.X, self.y))
self.testJ.append(self.N.costFunction(self.testX, self.testY))
def costFunctionWrapper(self, params, X, y):
self.N.setParams(params)
cost = self.N.costFunction(X, y)
grad = self.N.computeGradients(X,y)
return cost, grad
def train(self, trainX, trainY, testX, testY):
#Make an internal variable for the callback function:
self.X = trainX
self.y = trainY
self.testX = testX
self.testY = testY
#Make empty list to store training costs:
self.J = []
self.testJ = []
params0 = self.N.getParams()
options = {'maxiter': 200, 'disp' : True}
_res = optimize.minimize(self.costFunctionWrapper, params0, jac=True, method='BFGS', \
args=(trainX, trainY), options=options, callback=self.callbackF)
self.N.setParams(_res.x)
self.optimizationResults = _res
#Train network with new data:
NN = Neural_Network()
T = trainer(NN)
T.train(trainX, trainY, testX, testY)
#Plot cost during training:
plot(T.J)
plot(T.testJ)
grid(1)
xlabel('Iterations')
ylabel('Cost')
We can see that our model is overfitting our data around iteration 20-40. How can we use this data to penalize our model for overfitting? One solution is to introduce a "Regularization" parameter, lambda to our function. This value of lambda will allow us to tune our cost function. As lambda gets too big, bigger penalties will be imposed on our model.
#New complete class, with changes:
class Neural_Network(object):
def __init__(self, Lambda=0):
#Define Hyperparameters
self.inputLayerSize = 2
self.outputLayerSize = 1
self.hiddenLayerSize = 3
#Weights (parameters)
self.W1 = np.random.randn(self.inputLayerSize,self.hiddenLayerSize)
self.W2 = np.random.randn(self.hiddenLayerSize,self.outputLayerSize)
#Regularization Parameter:
self.Lambda = Lambda
def forward(self, X):
#Propogate inputs though network
self.z2 = np.dot(X, self.W1)
self.a2 = self.sigmoid(self.z2)
self.z3 = np.dot(self.a2, self.W2)
yHat = self.sigmoid(self.z3)
return yHat
def sigmoid(self, z):
#Apply sigmoid activation function to scalar, vector, or matrix
return 1/(1+np.exp(-z))
def sigmoidPrime(self,z):
#Gradient of sigmoid
return np.exp(-z)/((1+np.exp(-z))**2)
def costFunction(self, X, y):
#Compute cost for given X,y, use weights already stored in class.
self.yHat = self.forward(X)
J = 0.5*sum((y-self.yHat)**2)/X.shape[0] + (self.Lambda/2)*(sum(self.W1**2)+sum(self.W2**2))
return J
def costFunctionPrime(self, X, y):
#Compute derivative with respect to W and W2 for a given X and y:
self.yHat = self.forward(X)
delta3 = np.multiply(-(y-self.yHat), self.sigmoidPrime(self.z3))
#Add gradient of regularization term:
dJdW2 = np.dot(self.a2.T, delta3)/X.shape[0] + self.Lambda*self.W2
delta2 = np.dot(delta3, self.W2.T)*self.sigmoidPrime(self.z2)
#Add gradient of regularization term:
dJdW1 = np.dot(X.T, delta2)/X.shape[0] + self.Lambda*self.W1
return dJdW1, dJdW2
#Helper functions for interacting with other methods/classes
def getParams(self):
#Get W1 and W2 Rolled into vector:
params = np.concatenate((self.W1.ravel(), self.W2.ravel()))
return params
def setParams(self, params):
#Set W1 and W2 using single parameter vector:
W1_start = 0
W1_end = self.hiddenLayerSize*self.inputLayerSize
self.W1 = np.reshape(params[W1_start:W1_end], \
(self.inputLayerSize, self.hiddenLayerSize))
W2_end = W1_end + self.hiddenLayerSize*self.outputLayerSize
self.W2 = np.reshape(params[W1_end:W2_end], \
(self.hiddenLayerSize, self.outputLayerSize))
def computeGradients(self, X, y):
dJdW1, dJdW2 = self.costFunctionPrime(X, y)
return np.concatenate((dJdW1.ravel(), dJdW2.ravel()))
NN = Neural_Network(Lambda=0.001)
#Make sure our gradients our correct after making changes:
numgrad = computeNumericalGradient(NN, X, y)
grad = NN.computeGradients(X,y)
#Should be less than 1e-8:
norm(grad-numgrad)/norm(grad+numgrad)
T = trainer(NN)
T.train(X,y,testX,testY)
plot(T.J)
plot(T.testJ)
grid(1)
xlabel('Iterations')
ylabel('Cost')
allOutputs = NN.forward(allInputs)
#Contour Plot:
yy = np.dot(hoursStudy.reshape(100,1), np.ones((1,100)))
xx = np.dot(hoursSleep.reshape(100,1), np.ones((1,100))).T
CS = contour(xx,yy,100*allOutputs.reshape(100, 100))
clabel(CS, inline=1, fontsize=10)
xlabel('Hours Sleep')
ylabel('Hours Study')
#3D plot:
##Uncomment to plot out-of-notebook (you'll be able to rotate)
#%matplotlib qt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.scatter(10*X[:,0], 5*X[:,1], 100*y, c='k', alpha = 1, s=30)
surf = ax.plot_surface(xx, yy, 100*allOutputs.reshape(100, 100), \
cmap=cm.jet, alpha = 0.5)
ax.set_xlabel('Hours Sleep')
ax.set_ylabel('Hours Study')
ax.set_zlabel('Test Score')
With the regularization parameter added, we can see that our model is not interested in exactly fitting our data anymore, our training and testing errors are closer, and we have reduced overfitting on our model. We can further reduce overfitting by increasing and tuning lambda.
MNIST and Neural Nets in Practice
There are many factors that determine how a neural network will function. One of these factors is your computer. Because neural networks are a mix of brute force and finesse, they will tax your computer if your dataset is large enough. This is the issue I ran into when I attempted to learn TensorFlow. I went through the first tutorials up until MNIST, and discovered that their digit recognition example takes about twenty minutes to run on my computer, which just will not do. My solution was to do more research into the open source neural network libraries, which seem to (like most other software), perform better than their enterprise counterparts.
I found that the library Theano, used by Spotify and Torch, used by facebook have cult followings that make them superior to tensorflow. Theano, being a symbolic math language, was developed and is maintained by academics and offers superior functionality and expression to TensorFlow in my opinion. Torch is a well documented version of TensorFlow which also has a great neural network library. As an example of what Theano is capable of, check out this Spotify employee's open source Music Reccomendation Neural Network.
In addition to switching libraries, I found a way to accelerate my calculations on my GPU. Because my computer has a graphics card that is not integrated into the cpu, I am able to use NVIDIA's GPU wrapper library CUDA to speed up my programs. Theano and Torch were built on top of CUDA and is meant to perform seamlessly with GPU acceleration. As an added bonus, all of this functionality can be hooked by CPython within Ipython Notebook!
Theano Documentation and Citations
Testing and Verifying GPU Acceleration
from theano import function, config, shared, sandbox
import theano.tensor as T
import numpy
import time
import theano.sandbox.cuda
theano.sandbox.cuda.use("cpu")
config.floatX = 'float64'
vlen = 10 * 30 * 768 # 10 x #cores x # threads per core
iters = 1000
rng = numpy.random.RandomState(22)
x = shared(numpy.asarray(rng.rand(vlen), config.floatX))
f = function([], T.exp(x))
print(f.maker.fgraph.toposort())
t0 = time.time()
for i in range(iters):
r = f()
t1 = time.time()
print("Looping %d times took %f seconds" % (iters, t1 - t0))
print("Result is %s" % (r,))
if numpy.any([isinstance(x.op, T.Elemwise) for x in f.maker.fgraph.toposort()]):
print('Used the cpu')
else:
print('Used the gpu')
The example above is one I modified from the Theano Doc's to show the difference between using the GPU and CPU. Theano has a configuration file for settings you would like to be rather permanent, and also allows you to call those settings from within python. By setting theano.sandbox.cuda.use("cpu"), I force the computer to do the calculations on the CPU, regardless of the priority device. Additionally, Theano like's its information to be in float32 format to increase speed. Here I forced config.floatX = 'float64'. As you can see, the code for this program ran in about 5 seconds.
from theano import function, config, shared, sandbox
import theano.tensor as T
import numpy
import time
import theano.sandbox.cuda
theano.sandbox.cuda.use("gpu")
config.floatX = 'float32'
vlen = 10 * 30 * 768 # 10 x #cores x # threads per core
iters = 1000
rng = numpy.random.RandomState(22)
x = shared(numpy.asarray(rng.rand(vlen), config.floatX))
f = function([], T.exp(x), mode = 'FAST_RUN')
print(f.maker.fgraph.toposort())
t0 = time.time()
for i in range(iters):
r = f()
t1 = time.time()
print("Looping %d times took %f seconds" % (iters, t1 - t0))
print("Result is %s" % (r,))
if numpy.any([isinstance(x.op, T.Elemwise) for x in f.maker.fgraph.toposort()]):
print('Used the cpu')
else:
print('Used the gpu')
print(theano.config.device)
print(theano.config.mode)
By forcing the theano.sandbox.cuda.use("gpu"), config.floatX = 'float32', and mode = 'FAST_RUN', we can drastically speed up our calculations. As you can see, this program ran in under 2 seconds, about half to 3/4 as long as the previous example.
In Practice
Since I had some extra time over spring break, I decided to try and write a program that would take a picture of a handwritten digit, train a neural network on the MNIST Dataset, and offer a prediction of the handwritten digit at the end. Additionally, I wanted to do all of this with GPU acceleration, hosted on my Ipython Notebook Server. This meant gaining an in depth understanding of how Ipython uses dependencies, and how my computer uses python dist-packages. Through much trial, I compiled a python3 compatible version of OpenCV2, and linked it to the python dist-packages, allowing it to be used within Ipython. I had to do the same with theano, and cudaNN. The end result is a beautiful workflow that allows you to train neural networks, take pictures and do image manipulation, and use markdown all within your IDE, sped up by the GPU.
The MNIST Dataset is famously hosted on Yann Lecunn's website, and can be downloaded for free here.
*Note, restart kernel before you run this script to unimport pylab inline.
#Capture Test Sample
#Necessary Imports
import os
import sys
import numpy as np
import cv2
from matplotlib import pyplot as plt
from matplotlib.patches import Rectangle
#Verify that we are using opencv version 3
print("Using OpenCV Version",cv2.__version__)
#cmdstring = "espeak 'Hello, Please hold a picture of a handwritten digit up to the webcam.'"
#os.system(cmdstring)
# Camera 0 is the integrated web cam on my netbook
#camera_port = 0
#Let camera adjust for light levels
#ramp_frames = 30
# Now we can initialize the camera capture object with the cv2.VideoCapture class.
# All it needs is the index to a camera port.
#camera = cv2.VideoCapture(camera_port)
# Captures a single image from the camera and returns it in PIL format
#cmdstring = "espeak 'Please drag the rectangle over the handwritten digit. When you are satisfied with the center, click the red X to exit.'"
#os.system(cmdstring)
def get_image():
#read is the easiest way to get a full image out of a VideoCapture object.
retval, im = camera.read()
return im
# Ramp the camera - these frames will be discarded and are only used to allow v4l2
# to adjust light levels, if necessary
#for i in range(ramp_frames):
# temp = get_image()
#print("Taking image...")
# Take the actual image we want to keep
#capture = get_image()
#file = "test_image.png"
# A nice feature of the imwrite method is that it will automatically choose the
# correct format based on the file extension you provide. Convenient!
#cv2.imwrite(file, capture)
# You'll want to release the camera, otherwise you won't be able to create a new
# capture object until your script exits
#del(camera)
#Create a class that will contain callbacks within our image.
class DraggableRectangle:
#Initialize the rectangle
def __init__(self, rect):
self.rect = rect
self.press = None
#Connect mouse listener to rectangle
def connect(self):
'connect to all the events we need'
self.cidpress = self.rect.figure.canvas.mpl_connect(
'button_press_event', self.on_press)
self.cidrelease = self.rect.figure.canvas.mpl_connect(
'button_release_event', self.on_release)
self.cidmotion = self.rect.figure.canvas.mpl_connect(
'motion_notify_event', self.on_motion)
def on_press(self, event):
'on button press we will see if the mouse is over us and store some data'
if event.inaxes != self.rect.axes: return
contains, attrd = self.rect.contains(event)
if not contains: return
print ('event contains', self.rect.xy)
x0, y0 = self.rect.xy
self.press = x0, y0, event.xdata, event.ydata
def on_motion(self, event):
'on motion we will move the rect if the mouse is over us'
if self.press is None: return
if event.inaxes != self.rect.axes: return
x0, y0, xpress, ypress = self.press
dx = event.xdata - xpress
dy = event.ydata - ypress
self.rect.set_x(x0+dx)
self.rect.set_y(y0+dy)
self.rect.figure.canvas.draw()
def on_release(self, event):
'on release we reset the press data'
self.press = None
self.rect.figure.canvas.draw()
newClip.X, newClip.Y = event.x-14, event.y
def disconnect(self):
'disconnect all the stored connection ids'
self.rect.figure.canvas.mpl_disconnect(self.cidpress)
self.rect.figure.canvas.mpl_disconnect(self.cidrelease)
self.rect.figure.canvas.mpl_disconnect(self.cidmotion)
#Clip object to store center points of full image
class NewClip:
def __init__(self, X, Y):
self.X = X
self.Y = Y
#Set our clip to the middle of the image
#newClip = NewClip((640/2),(480/2))
#img = cv2.imread('test_image.png',0)
#print(img.shape)
#fig = plt.figure()
#Display image with inverse grey scale...gray? make up your fucking mind english.
#plt.imshow(img, cmap = 'Greys')
#ax = plt.subplot()
#currentAxis = plt.gca()
#rect = Rectangle((newClip.X, newClip.Y), 28, 28,
# alpha=.5, facecolor='white')
#print(newClip.X, newClip.Y)
#currentAxis.add_patch(rect)
#dr = DraggableRectangle(rect)
#dr.connect()
#plt.show()
#Show center points
#print(newClip.X, newClip.Y)
#clip = img[((480 - newClip.Y) -14):((480 - newClip.Y) + 14),
# ((newClip.X) - 14):((newClip.X) + 14)]
#Verify that our clip is the correct dimension
#print(clip.shape)
#plt.imshow(clip, cmap = 'gray')
#plt.show()
#cmdstring = "espeak 'If you are unsatisfied with the sample image, please restart the program.'"
#os.system(cmdstring)
In the above program, I wrote a method to grab a clip from a gray scale image the size of the MNIST images. This allows me to create my own test data. I will not go into detail on how I wrote the opencv program, as the focus is on neural networks, and it is quite well documented. The speech library I am using is espeak, for Ubuntu.
import numpy
import os
import sys
import numpy as np
import cv2
from matplotlib import pyplot as plt
from matplotlib.patches import Rectangle
from theano import function, config, shared, sandbox
import theano.tensor as T
import theano.sandbox.cuda
theano.sandbox.cuda.use("gpu")
config.floatX = 'float32'
cmdstring = "espeak 'Converting the test image to M N I S T format.'"
os.system(cmdstring)
# Uncomment to choose a new test image
#cv2.imwrite('one.png', clip)
testArray = cv2.imread('one.png', 0)
plt.imshow(testArray, 'gray')
plt.show()
print(testArray.shape)
def convert(image):
image2 = image.reshape((1, 784))
print(image2.shape)
print(image2)
for i in range(image2.size):
if image2[[0],[i]] >= 145:
image2[[0],[i]] = 0.
return image2
testArray = convert(testArray)
testArray = testArray/145
testArray = numpy.asarray(testArray, dtype=theano.config.floatX)
print(testArray)
errorCheck = testArray.reshape((28,28))
plt.imshow(errorCheck, 'gray')
plt.show()
The MNIST Data is stored in a very confusing packaging, so we need to convert the test clip into something our Neural Network will understand alongside the MNIST data. By reshaping the array to 1, 784 and using a threshhold function, we can replicate the black and white tensors stored in the pickle. Additionally, theano requires us to convert the data to float32 so this does not take forever.
cmdstring = "espeak 'Loading M N I S T dataset.'"
os.system(cmdstring)
import gzip, numpy
import pickle
f = gzip.open('mnist.pkl.gz', 'rb')
train_set, valid_set, test_set = pickle.load(f, encoding='iso-8859-1')
f.close()
Function from the theano docs to unpack MNIST Data.
cmdstring = "espeak 'Storing variables to G P U.'"
os.system(cmdstring)
from theano import function, config, shared, sandbox
import theano.tensor as T
import time
import theano.sandbox.cuda
theano.sandbox.cuda.use("gpu")
def shared_dataset(data_xy):
""" Function that loads the dataset into shared variables
The reason we store our dataset in shared variables is to allow
Theano to copy it into the GPU memory (when code is run on GPU).
Since copying data into the GPU is slow, copying a minibatch everytime
is needed (the default behaviour if the data is not in a shared
variable) would lead to a large decrease in performance.
"""
data_x, data_y = data_xy
shared_x = theano.shared(numpy.asarray(data_x, dtype=theano.config.floatX))
shared_y = theano.shared(numpy.asarray(data_y, dtype=theano.config.floatX))
# When storing data on the GPU it has to be stored as floats
# therefore we will store the labels as ``floatX`` as well
# (``shared_y`` does exactly that). But during our computations
# we need them as ints (we use labels as index, and if they are
# floats it doesn't make sense) therefore instead of returning
# ``shared_y`` we will have to cast it to int. This little hack
# lets us get around this issue
return shared_x, T.cast(shared_y, 'int32')
test_set_x, test_set_y = shared_dataset(test_set)
valid_set_x, valid_set_y = shared_dataset(valid_set)
train_set_x, train_set_y = shared_dataset(train_set)
batch_size = 500 # size of the minibatch
# accessing the third minibatch of the training set
data = train_set_x[2 * batch_size: 3 * batch_size]
label = train_set_y[2 * batch_size: 3 * batch_size]
Function from the theano docs to similarly store the MNIST Data in shared memory on the GPU, and split between test and training batches.
cmdstring = "espeak 'Training Neural Network on 50000 handwritten characters.'"
os.system(cmdstring)
#Teach our network to recognize handwritten digits
"""
This tutorial introduces logistic regression using Theano and stochastic
gradient descent.
Logistic regression is a probabilistic, linear classifier. It is parametrized
by a weight matrix :math:`W` and a bias vector :math:`b`. Classification is
done by projecting data points onto a set of hyperplanes, the distance to
which is used to determine a class membership probability.
Mathematically, this can be written as:
.. math::
P(Y=i|x, W,b) &= softmax_i(W x + b) \\
&= \frac {e^{W_i x + b_i}} {\sum_j e^{W_j x + b_j}}
The output of the model or prediction is then done by taking the argmax of
the vector whose i'th element is P(Y=i|x).
.. math::
y_{pred} = argmax_i P(Y=i|x,W,b)
This tutorial presents a stochastic gradient descent optimization method
suitable for large datasets.
References:
- textbooks: "Pattern Recognition and Machine Learning" -
Christopher M. Bishop, section 4.3.2
"""
from __future__ import print_function
__docformat__ = 'restructedtext en'
import six.moves.cPickle as pickle
import gzip
import os
import sys
import timeit
class LogisticRegression(object):
"""Multi-class Logistic Regression Class
The logistic regression is fully described by a weight matrix :math:`W`
and bias vector :math:`b`. Classification is done by projecting data
points onto a set of hyperplanes, the distance to which is used to
determine a class membership probability.
"""
def __init__(self, input, n_in, n_out):
""" Initialize the parameters of the logistic regression
:type input: theano.tensor.TensorType
:param input: symbolic variable that describes the input of the
architecture (one minibatch)
:type n_in: int
:param n_in: number of input units, the dimension of the space in
which the datapoints lie
:type n_out: int
:param n_out: number of output units, the dimension of the space in
which the labels lie
"""
# start-snippet-1
# initialize with 0 the weights W as a matrix of shape (n_in, n_out)
self.W = theano.shared(
value=numpy.zeros(
(n_in, n_out),
dtype=theano.config.floatX
),
name='W',
borrow=True
)
# initialize the biases b as a vector of n_out 0s
self.b = theano.shared(
value=numpy.zeros(
(n_out,),
dtype=theano.config.floatX
),
name='b',
borrow=True
)
print(theano.config.floatX)
print(theano.config.mode)
print(theano.config.device)
# symbolic expression for computing the matrix of class-membership
# probabilities
# Where:
# W is a matrix where column-k represent the separation hyperplane for
# class-k
# x is a matrix where row-j represents input training sample-j
# b is a vector where element-k represent the free parameter of
# hyperplane-k
self.p_y_given_x = T.nnet.softmax(T.dot(input, self.W) + self.b)
# symbolic description of how to compute prediction as class whose
# probability is maximal
self.y_pred = T.argmax(self.p_y_given_x, axis=1)
# end-snippet-1
# parameters of the model
self.params = [self.W, self.b]
# keep track of model input
self.input = input
def negative_log_likelihood(self, y):
"""Return the mean of the negative log-likelihood of the prediction
of this model under a given target distribution.
.. math::
\frac{1}{|\mathcal{D}|} \mathcal{L} (\theta=\{W,b\}, \mathcal{D}) =
\frac{1}{|\mathcal{D}|} \sum_{i=0}^{|\mathcal{D}|}
\log(P(Y=y^{(i)}|x^{(i)}, W,b)) \\
\ell (\theta=\{W,b\}, \mathcal{D})
:type y: theano.tensor.TensorType
:param y: corresponds to a vector that gives for each example the
correct label
Note: we use the mean instead of the sum so that
the learning rate is less dependent on the batch size
"""
# start-snippet-2
# y.shape[0] is (symbolically) the number of rows in y, i.e.,
# number of examples (call it n) in the minibatch
# T.arange(y.shape[0]) is a symbolic vector which will contain
# [0,1,2,... n-1] T.log(self.p_y_given_x) is a matrix of
# Log-Probabilities (call it LP) with one row per example and
# one column per class LP[T.arange(y.shape[0]),y] is a vector
# v containing [LP[0,y[0]], LP[1,y[1]], LP[2,y[2]], ...,
# LP[n-1,y[n-1]]] and T.mean(LP[T.arange(y.shape[0]),y]) is
# the mean (across minibatch examples) of the elements in v,
# i.e., the mean log-likelihood across the minibatch.
return -T.mean(T.log(self.p_y_given_x)[T.arange(y.shape[0]), y])
# end-snippet-2
def errors(self, y):
"""Return a float representing the number of errors in the minibatch
over the total number of examples of the minibatch ; zero one
loss over the size of the minibatch
:type y: theano.tensor.TensorType
:param y: corresponds to a vector that gives for each example the
correct label
"""
# check if y has same dimension of y_pred
if y.ndim != self.y_pred.ndim:
raise TypeError(
'y should have the same shape as self.y_pred',
('y', y.type, 'y_pred', self.y_pred.type)
)
# check if y is of the correct datatype
if y.dtype.startswith('int'):
# the T.neq operator returns a vector of 0s and 1s, where 1
# represents a mistake in prediction
return T.mean(T.neq(self.y_pred, y))
else:
raise NotImplementedError()
def load_data(dataset):
''' Loads the dataset
:type dataset: string
:param dataset: the path to the dataset (here MNIST)
'''
#############
# LOAD DATA #
#############
# Download the MNIST dataset if it is not present
data_dir, data_file = os.path.split(dataset)
if data_dir == "" and not os.path.isfile(dataset):
# Check if dataset is in the data directory.
new_path = os.path.join(
os.path.split(__file__)[0],
"..",
"data",
dataset
)
if os.path.isfile(new_path) or data_file == 'mnist.pkl.gz':
dataset = new_path
if (not os.path.isfile(dataset)) and data_file == 'mnist.pkl.gz':
from six.moves import urllib
origin = (
'http://www.iro.umontreal.ca/~lisa/deep/data/mnist/mnist.pkl.gz'
)
print('Downloading data from %s' % origin)
urllib.request.urlretrieve(origin, dataset)
print('... loading data')
# Load the dataset
with gzip.open(dataset, 'rb') as f:
try:
train_set, valid_set, test_set = pickle.load(f, encoding='latin1')
except:
train_set, valid_set, test_set = pickle.load(f)
# train_set, valid_set, test_set format: tuple(input, target)
# input is a numpy.ndarray of 2 dimensions (a matrix)
# where each row corresponds to an example. target is a
# numpy.ndarray of 1 dimension (vector) that has the same length as
# the number of rows in the input. It should give the target
# to the example with the same index in the input.
def shared_dataset(data_xy, borrow=True):
""" Function that loads the dataset into shared variables
The reason we store our dataset in shared variables is to allow
Theano to copy it into the GPU memory (when code is run on GPU).
Since copying data into the GPU is slow, copying a minibatch everytime
is needed (the default behaviour if the data is not in a shared
variable) would lead to a large decrease in performance.
"""
data_x, data_y = data_xy
shared_x = theano.shared(numpy.asarray(data_x,
dtype=theano.config.floatX),
borrow=borrow)
shared_y = theano.shared(numpy.asarray(data_y,
dtype=theano.config.floatX),
borrow=borrow)
# When storing data on the GPU it has to be stored as floats
# therefore we will store the labels as ``floatX`` as well
# (``shared_y`` does exactly that). But during our computations
# we need them as ints (we use labels as index, and if they are
# floats it doesn't make sense) therefore instead of returning
# ``shared_y`` we will have to cast it to int. This little hack
# lets ous get around this issue
return shared_x, T.cast(shared_y, 'int32')
test_set_x, test_set_y = shared_dataset(test_set)
valid_set_x, valid_set_y = shared_dataset(valid_set)
train_set_x, train_set_y = shared_dataset(train_set)
rval = [(train_set_x, train_set_y), (valid_set_x, valid_set_y),
(test_set_x, test_set_y)]
return rval
def sgd_optimization_mnist(learning_rate=0.13, n_epochs=1000,
dataset='mnist.pkl.gz',
batch_size=600):
"""
Demonstrate stochastic gradient descent optimization of a log-linear
model
This is demonstrated on MNIST.
:type learning_rate: float
:param learning_rate: learning rate used (factor for the stochastic
gradient)
:type n_epochs: int
:param n_epochs: maximal number of epochs to run the optimizer
:type dataset: string
:param dataset: the path of the MNIST dataset file from
http://www.iro.umontreal.ca/~lisa/deep/data/mnist/mnist.pkl.gz
"""
datasets = load_data(dataset)
train_set_x, train_set_y = datasets[0]
valid_set_x, valid_set_y = datasets[1]
test_set_x, test_set_y = datasets[2]
# compute number of minibatches for training, validation and testing
n_train_batches = train_set_x.get_value(borrow=True).shape[0] // batch_size
n_valid_batches = valid_set_x.get_value(borrow=True).shape[0] // batch_size
n_test_batches = test_set_x.get_value(borrow=True).shape[0] // batch_size
######################
# BUILD ACTUAL MODEL #
######################
print('... building the model')
# allocate symbolic variables for the data
index = T.lscalar() # index to a [mini]batch
# generate symbolic variables for input (x and y represent a
# minibatch)
x = T.matrix('x') # data, presented as rasterized images
y = T.ivector('y') # labels, presented as 1D vector of [int] labels
# construct the logistic regression class
# Each MNIST image has size 28*28
classifier = LogisticRegression(input=x, n_in=28 * 28, n_out=10)
# the cost we minimize during training is the negative log likelihood of
# the model in symbolic format
cost = classifier.negative_log_likelihood(y)
# compiling a Theano function that computes the mistakes that are made by
# the model on a minibatch
test_model = theano.function(
inputs=[index],
outputs=classifier.errors(y),
givens={
x: test_set_x[index * batch_size: (index + 1) * batch_size],
y: test_set_y[index * batch_size: (index + 1) * batch_size]
}
,mode = "FAST_RUN")
validate_model = theano.function(
inputs=[index],
outputs=classifier.errors(y),
givens={
x: valid_set_x[index * batch_size: (index + 1) * batch_size],
y: valid_set_y[index * batch_size: (index + 1) * batch_size]
}
,mode = "FAST_RUN")
# compute the gradient of cost with respect to theta = (W,b)
g_W = T.grad(cost=cost, wrt=classifier.W)
g_b = T.grad(cost=cost, wrt=classifier.b)
# start-snippet-3
# specify how to update the parameters of the model as a list of
# (variable, update expression) pairs.
updates = [(classifier.W, classifier.W - learning_rate * g_W),
(classifier.b, classifier.b - learning_rate * g_b)]
# compiling a Theano function `train_model` that returns the cost, but in
# the same time updates the parameter of the model based on the rules
# defined in `updates`
train_model = theano.function(
inputs=[index],
outputs=cost,
updates=updates,
givens={
x: train_set_x[index * batch_size: (index + 1) * batch_size],
y: train_set_y[index * batch_size: (index + 1) * batch_size]
}
, mode = "FAST_RUN")
print(theano.config.floatX)
print(theano.config.mode)
print(theano.config.device)
# end-snippet-3
###############
# TRAIN MODEL #
###############
print('... training the model')
# early-stopping parameters
patience = 5000 # look as this many examples regardless
patience_increase = 2 # wait this much longer when a new best is
# found
improvement_threshold = 0.995 # a relative improvement of this much is
# considered significant
validation_frequency = min(n_train_batches, patience // 2)
# go through this many
# minibatche before checking the network
# on the validation set; in this case we
# check every epoch
best_validation_loss = numpy.inf
test_score = 0.
start_time = timeit.default_timer()
done_looping = False
epoch = 0
while (epoch < n_epochs) and (not done_looping):
epoch = epoch + 1
for minibatch_index in range(n_train_batches):
minibatch_avg_cost = train_model(minibatch_index)
# iteration number
iter = (epoch - 1) * n_train_batches + minibatch_index
if (iter + 1) % validation_frequency == 0:
# compute zero-one loss on validation set
validation_losses = [validate_model(i)
for i in range(n_valid_batches)]
this_validation_loss = numpy.mean(validation_losses)
print(
'epoch %i, minibatch %i/%i, validation error %f %%' %
(
epoch,
minibatch_index + 1,
n_train_batches,
this_validation_loss * 100.
)
)
print(theano.config.floatX)
print(theano.config.mode)
print(theano.config.device)
# if we got the best validation score until now
if this_validation_loss < best_validation_loss:
#improve patience if loss improvement is good enough
if this_validation_loss < best_validation_loss * \
improvement_threshold:
patience = max(patience, iter * patience_increase)
best_validation_loss = this_validation_loss
# test it on the test set
test_losses = [test_model(i)
for i in range(n_test_batches)]
test_score = numpy.mean(test_losses)
print(
(
' epoch %i, minibatch %i/%i, test error of'
' best model %f %%'
) %
(
epoch,
minibatch_index + 1,
n_train_batches,
test_score * 100.
)
)
# save the best model
with open('best_model.pkl', 'wb') as f:
pickle.dump(classifier, f)
if patience <= iter:
done_looping = True
break
end_time = timeit.default_timer()
print(
(
'Optimization complete with best validation score of %f %%,'
'with test performance %f %%'
)
% (best_validation_loss * 100., test_score * 100.)
)
print('The code run for %d epochs, with %f epochs/sec' % (
epoch, 1. * epoch / (end_time - start_time)))
print(('The code for file ' +
os.path.split('__file__')[1] +
' ran for %.1fs' % ((end_time - start_time))), file=sys.stderr)
sgd_optimization_mnist()
print(theano.config.floatX)
print(theano.config.mode)
print(theano.config.device)
Above is the Neural Network I plan to modify next week to use convolutional pooling. As you can see, the code uses the GPU, and runs in under 25 seconds, which is quite reasonable for 50,000 data inputs!
cmdstring = "espeak 'Evaluating model and predicting label for test image.'"
os.system(cmdstring)
def predict():
"""
An example of how to load a trained model and use it
to predict labels.
"""
# load the saved model
classifier = pickle.load(open('best_model.pkl', 'rb'))
# compile a predictor function
predict_model = theano.function(
inputs=[classifier.input],
outputs=classifier.y_pred)
# We can test it on some examples from test set
dataset='mnist.pkl.gz'
datasets = load_data(dataset)
test_set_x, test_set_y = datasets[2]
test_set_x = test_set_x.get_value()
predicted_values = predict_model(test_set_x[:10])
print("Predicted values for the first 10 examples in test set:")
print(predicted_values)
predicted_values2 = predict_model(testArray)
print("Predicted value for test sample:")
print(predicted_values2)
errorCheck = testArray.reshape((28,28))
plt.imshow(errorCheck, 'gray')
plt.show()
errorCheck2 = test_set_x[2].reshape((28,28))
plt.imshow(errorCheck2, 'gray')
plt.show()
predict()
This function checks our test image, and the first ten provided test images againste the neural network's best epoch, or training dataset. As you can see, the program is correctly recognizing the provided data, but incorrectly categorizing my test image. I believe this is due to the small size of the clips (it makes it hard to get a perfectly centered image), and my threshholding function. Because the data are 1d arrays, uniformity is imperative. One way to account for this uniformity is to use what is called convolutional pooling on your image. Pooling is breaking the image down into different sections like our visual cortex does. This helps the neural network learn even if the images are off center or at an angle or rotated.
import numpy as np
import theano
import theano.tensor as T
import lasagne
import matplotlib.pyplot as plt
import gzip
import pickle
# Seed for reproduciblity
np.random.seed(42)
f = gzip.open('mnist.pkl.gz', 'rb')
train, val, test = pickle.load(f, encoding='iso-8859-1')
#train, val, test = pickle.load(gzip.open('mnist.pkl.gz'))
X_train, y_train = train
X_val, y_val = val
def batch_gen(X, y, N):
while True:
idx = np.random.choice(len(y), N)
yield X[idx].astype('float32'), y[idx].astype('int32')
# We need to reshape from a 1D feature vector to a 1 channel 2D image.
# Then we apply 3 convolutional filters with 3x3 kernel size.
l_in = lasagne.layers.InputLayer((None, 784))
l_shape = lasagne.layers.ReshapeLayer(l_in, (-1, 1, 28, 28))
l_conv = lasagne.layers.Conv2DLayer(l_shape, num_filters=3, filter_size=3, pad=1)
l_out = lasagne.layers.DenseLayer(l_conv,
num_units=10,
nonlinearity=lasagne.nonlinearities.softmax)
X_sym = T.matrix()
y_sym = T.ivector()
output = lasagne.layers.get_output(l_out, X_sym)
pred = output.argmax(-1)
loss = T.mean(lasagne.objectives.categorical_crossentropy(output, y_sym))
acc = T.mean(T.eq(pred, y_sym))
params = lasagne.layers.get_all_params(l_out)
grad = T.grad(loss, params)
updates = lasagne.updates.adam(grad, params, learning_rate=0.005)
f_train = theano.function([X_sym, y_sym], [loss, acc], updates=updates)
f_val = theano.function([X_sym, y_sym], [loss, acc])
f_predict = theano.function([X_sym], pred)
BATCH_SIZE = 600
N_BATCHES = len(X_train) // BATCH_SIZE
N_VAL_BATCHES = len(X_val) // BATCH_SIZE
train_batches = batch_gen(X_train, y_train, BATCH_SIZE)
val_batches = batch_gen(X_val, y_val, BATCH_SIZE)
for epoch in range(8):
train_loss = 0
train_acc = 0
for _ in range(N_BATCHES):
X, y = next(train_batches)
loss, acc = f_train(X, y)
train_loss += loss
train_acc += acc
train_loss /= N_BATCHES
train_acc /= N_BATCHES
val_loss = 0
val_acc = 0
for _ in range(N_VAL_BATCHES):
X, y = next(val_batches)
loss, acc = f_val(X, y)
val_loss += loss
val_acc += acc
val_loss /= N_VAL_BATCHES
val_acc /= N_VAL_BATCHES
print('Epoch {:2d}, Train loss {:.03f} (validation : {:.03f}) ratio {:.03f}'.format(
epoch, train_loss, val_loss, val_loss/train_loss))
print(' Train accuracy {:.03f} (validation : {:.03f})'.format(train_acc, val_acc))
print("DONE")
filtered = lasagne.layers.get_output(l_conv, X_sym)
f_filter = theano.function([X_sym], filtered)
# Filter the first few training examples
im = f_filter(X_train[:10])
print(im.shape)
# Rearrange dimension so we can plot the result as RGB images
im = np.rollaxis(np.rollaxis(im, 3, 1), 3, 1)
plt.figure(figsize=(16,8))
for i in range(10):
plt.subplot(1, 10, i+1)
plt.imshow(im[i], interpolation='nearest')
plt.axis('off')
im = f_filter(errorCheck)
im = np.rollaxis(np.rollaxis(im, 3, 1), 3, 1)
plt.figure(figsize=(16,8))
for i in range(1):
plt.subplot(1, 10, i+1)
plt.imshow(im[i], interpolation='nearest')
plt.axis('off')
print(f_predict(X_train[6:7]))
print(f_predict(testArray))